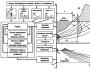
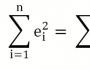Апроксимація досвідчених даних. Метод найменших квадратів. Апроксимація функції методом найменших квадратів Використовуючи метод найменших квадратів апроксимувати
Після вирівнювання отримаємо функцію наступного виду: g(x) = x + 1 3 + 1 .
Ми можемо апроксимувати ці дані за допомогою лінійної залежності y = a x + b, обчисливши відповідні параметри. Для цього нам потрібно буде застосувати так званий спосіб найменших квадратів. Також потрібно зробити креслення, щоб перевірити, яка лінія краще вирівнюватиме експериментальні дані.
У чому полягає МНК (метод найменших квадратів)
Головне, що нам потрібно зробити – це знайти такі коефіцієнти лінійної залежності, при яких значення функції двох змінних F (a, b) = ∑ i = 1 n (y i - (a x i + b)) 2 буде найменшим. Інакше кажучи, при певних значеннях a і b сума квадратів відхилень представлених даних від прямої буде мати мінімальне значення. У цьому полягає сенс методу найменших квадратів. Все, що нам треба зробити для вирішення прикладу, – це знайти екстремум функції двох змінних.
Як вивести формули для обчислення коефіцієнтів
Щоб вивести формули для обчислення коефіцієнтів, потрібно скласти і вирішити систему рівнянь з двома змінними. Для цього ми обчислюємо приватні похідні вирази F (a , b) = ∑ i = 1 n (y i - (a x i + b)) 2 a і b і прирівнюємо їх до 0 .
δ F (a , b) δ a = 0 δ F (a , b) δ b = 0 ⇔ - 2 ∑ i = 1 n (yi - (axi + b)) xi = 0 - 2 ∑ i = 1 n ( yi - (axi + b)) = 0 ⇔ a ∑ i = 1 nxi 2 + b ∑ i = 1 nxi = ∑ i = 1 nxiyia ∑ i = 1 nxi + ∑ i = 1 nb = ∑ i = 1 nyi ⇔ ∑ i = 1 nxi 2 + b ∑ i = 1 nxi = ∑ i = 1 nxiyia ∑ i = 1 nxi + nb = ∑ i = 1 nyi
Для вирішення системи рівнянь можна використовувати будь-які методи, наприклад підстановку або метод Крамера. У результаті маємо вийти формули, з допомогою яких обчислюються коефіцієнти методом найменших квадратів.
n ∑ i = 1 n x i y i - ∑ i = 1 n x i ∑ i = 1 n i i n ∑ i = 1 n - ∑ i = 1 n x i 2 b = ∑ i = 1 n y i - a ∑ i = 1 n x i n
Ми вирахували значення змінних, при яких функція
F (a , b) = ∑ i = 1 n (y i - (a x i + b)) 2 набуде мінімального значення. У третьому пункті ми доведемо, чому воно є таким.
Це і є застосування методу найменших квадратів на практиці. Його формула, яка застосовується для пошуку параметра a включає ∑ i = 1 n x i , ∑ i = 1 n y i , ∑ i = 1 n x i y i , ∑ i = 1 n x i 2 , а також параметр
n – їм зазначено кількість експериментальних даних. Радимо вам обчислювати кожну суму окремо. Значення коефіцієнта b обчислюється відразу після a.
Звернемося знову до прикладу.
Приклад 1
Тут у нас n дорівнює п'яти. Щоб було зручніше обчислювати потрібні суми, що входять до формул коефіцієнтів, заповнимо таблицю.
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | ∑ i = 1 5 | |
| x i | 0 | 1 | 2 | 4 | 5 | 12 |
| y i | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 | 12 , 9 |
| x i y i | 0 | 2 , 4 | 5 , 2 | 11 , 2 | 15 | 33 , 8 |
| x i 2 | 0 | 1 | 4 | 16 | 25 | 46 |
Рішення
Четвертий рядок включає дані, отримані при множенні значень з другого рядка на значення третього для кожного окремого i . П'ятий рядок містить дані з другого, зведені у квадрат. В останньому стовпці наводяться суми значень окремих рядків.
Скористаємося методом найменших квадратів, щоб обчислити потрібні нам коефіцієнти a і b. Для цього підставимо потрібні значення з останнього стовпця та підрахуємо суми:
n ∑ i = 1 nxiyi - ∑ i = 1 nxi ∑ i = 1 nyin ∑ i = 1 n - ∑ i = 1 nxi 2 b = ∑ i = 1 nyi - a ∑ i = 1 nxin ⇒ a = 5 · 3 8 - 12 · 12 , 9 5 · 46 - 12 2 b = 12 , 9 - a · 12 5 ⇒ a ≈ 0 , 165 b ≈ 2 , 184
У нас вийшло, що потрібна пряма апроксимує виглядатиме як y = 0 , 165 x + 2 , 184 . Тепер нам треба визначити, яка лінія краще апроксимувати дані – g (x) = x + 1 3 + 1 або 0 , 165 x + 2 , 184 . Зробимо оцінку за допомогою методу найменших квадратів.
Щоб вирахувати похибку, нам треба знайти суми квадратів відхилень даних від прямих σ 1 = ∑ i = 1 n (yi - (axi + bi)) 2 і σ 2 = ∑ i = 1 n (yi - g (xi)) 2 , мінімальне значення буде відповідати більш потрібній лінії.
σ 1 = ∑ i = 1 n (yi - (axi + bi)) 2 = = ∑ i = 1 5 (yi - (0 , 165 xi + 2 , 184)) 2 ≈ 0 , 019 σ 2 = ∑ i = 1 n (yi - g (xi)) 2 = = ∑ i = 1 5 (yi - (xi + 1 3 + 1)) 2 ≈ 0 , 096
Відповідь:оскільки σ 1< σ 2 , то прямой, наилучшим образом аппроксимирующей исходные данные, будет
y = 0,165 x + 2,184.
Спосіб найменших квадратів наочно показаний на графічній ілюстрації. За допомогою червоної лінії відзначено пряму g(x) = x + 1 3 + 1 , синю – y = 0 , 165 x + 2 , 184 . Вихідні дані позначені рожевими крапками.
Пояснимо, для чого саме потрібні наближення такого виду.
Вони можуть бути використані в завданнях, що вимагають згладжування даних, а також у тих, де дані треба інтерполювати або екстраполювати. Наприклад, у задачі, розібраній вище, можна було б знайти значення спостерігається величини y при x = 3 або x = 6 . Таким прикладам ми присвятили окрему статтю.
Доказ методу МНК
Щоб функція прийняла мінімальне значення при обчислених a і b потрібно, щоб у цій точці матриця квадратичної форми диференціала функції виду F (a, b) = ∑ i = 1 n (y i - (a x i + b)) 2 була позитивно визначеною. Покажемо, як це має виглядати.
Приклад 2
Ми маємо диференціал другого порядку наступного виду:
d 2 F (a ; b) = δ 2 F (a ; b) δ a 2 d 2 a + 2 δ 2 F (a ; b) δ a δ bdadb + δ 2 F (a ; b) δ b 2 d 2 b
Рішення
δ 2 F (a ; b) δ a 2 = δ δ F (a ; b) δ a δ a = = δ - 2 ∑ i = 1 n (yi - (axi + b)) xi δ a = 2 ∑ i = 1 n (xi) 2 δ 2 F (a ; b) δ a δ b = δ δ F (a ; b) δ a δ b = = δ - 2 ∑ i = 1 n (yi - (axi + b) ) xi δ b = 2 ∑ i = 1 nxi δ 2 F (a ; b) δ b 2 = δ δ F (a ; b) δ b δ b = δ - 2 ∑ i = 1 n (yi - (axi + b)) δ b = 2 ∑ i = 1 n (1) = 2 n
Інакше кажучи, можна записати так: d 2 F (a; b) = 2 ∑ i = 1 n (x i) 2 d 2 a + 2 · 2 ∑ x i i = 1 n d a d b + (2 n) d 2 b .
Ми отримали матрицю квадратичної форми виду M = 2 ∑ i = 1 n (x i) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n .
У цьому випадку значення окремих елементів не змінюватимуться залежно від a та b . Чи ця матриця є позитивно визначеною? Щоб відповісти на це питання, перевіримо, чи є її кутові мінори позитивними.
Обчислюємо кутовий мінор першого порядку: 2 ∑ i = 1 n (x i) 2 > 0 . Оскільки точки x i не збігаються, то нерівність є суворою. Матимемо це на увазі при подальших розрахунках.
Обчислюємо кутовий мінор другого порядку:
d e t (M) = 2 ∑ i = 1 n (x i) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n = 4 n ∑ i = 1 n (x i) 2 - ∑ i = 1 n x i 2
Після цього переходимо до доказу нерівності n ∑ i = 1 n (x i) 2 - ∑ i = 1 n x i 2 > 0 за допомогою математичної індукції.
- Перевіримо, чи буде ця нерівність справедливою за довільного n . Візьмемо 2 і підрахуємо:
2 ∑ i = 1 2 (xi) 2 - ∑ i = 1 2 xi 2 = 2 x 1 2 + x 2 2 - x 1 + x 2 2 = = x 1 2 - 2 x 1 x 2 + x 2 2 = x 1 + x 2 2 > 0
У нас вийшла правильна рівність (якщо значення x 1 і x 2 не співпадатимуть).
- Зробимо припущення, що це нерівність буде правильним для n, тобто. n ∑ i = 1 n (x i) 2 - ∑ i = 1 n x i 2 > 0 справедливо.
- Тепер доведемо справедливість за n + 1 , тобто . що (n + 1) ∑ i = 1 n + 1 (xi) 2 - ∑ i = 1 n + 1 xi 2 > 0, якщо вірно n ∑ i = 1 n (xi) 2 - ∑ i = 1 nxi 2 > 0 .
Обчислюємо:
(n + 1) ∑ i = 1 n + 1 (xi) 2 - ∑ i = 1 n + 1 xi 2 = = (n + 1) ∑ i = 1 n (xi) 2 + xn + 1 2 - ∑ i = 1 nxi + xn + 1 2 = = n ∑ i = 1 n (xi) 2 + n · xn + 1 2 + ∑ i = 1 n (xi) 2 + xn + 1 2 - - ∑ i = 1 nxi 2 + 2 xn + 1 ∑ i = 1 nxi + xn + 1 2 = = ∑ i = 1 n (xi) 2 - ∑ i = 1 nxi 2 + n · xn + 1 2 - xn + 1 ∑ i = 1 nxi + ∑ i = 1 n (xi) 2 = = ∑ i = 1 n (xi) 2 - ∑ i = 1 nxi 2 + xn + 1 2 - 2 xn + 1 x 1 + x 1 2 + + xn + 1 2 - 2 xn + 1 x 2 + x 2 2 +. . . + xn + 1 2 - 2 xn + 1 x 1 + xn 2 = = n ∑ i = 1 n (xi) 2 - ∑ i = 1 nxi 2 + + (xn + 1 - x 1) 2 + (xn + 1 - x 2) 2+. . . + (x n – 1 – x n) 2 > 0
Вираз, укладений у фігурні дужки, буде більше 0 (виходячи з того, що ми припускали в пункті 2), та інші доданки будуть більшими за 0, оскільки всі вони є квадратами чисел. Ми довели нерівність.
Відповідь:знайдені a і b відповідатимуть найменшому значенню функції F (a , b) = ∑ i = 1 n (y i - (a x i + b)) 2 , отже, є шуканими параметрами методу найменших квадратів (МНК).
Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter
Він має безліч застосувань, тому що дозволяє здійснювати наближене уявлення заданої функції більш простими. МНК може виявитися надзвичайно корисним при обробці спостережень, і його активно використовують з оцінки одних величин за результатами вимірювань інших, що містять випадкові помилки. З цієї статті ви дізнаєтеся, як реалізувати обчислення методом найменших квадратів в Excel.
Постановка задачі на конкретному прикладі
Припустимо, є два показники X і Y. Причому Y залежить від X. Оскільки МНК цікавить нас із погляду регресійного аналізу (в Excel його методи реалізуються з допомогою вбудованих функцій), варто відразу ж перейти до розгляду конкретного завдання.
Отже, нехай X - торгова площа продовольчого магазину, що вимірюється в квадратних метрах, а Y - річний товарообіг, який визначається мільйонами рублів.
Потрібно зробити прогноз, який товарообіг (Y) матиме магазин, якщо в нього та чи інша торгова площа. Вочевидь, що функція Y = f(X) зростаюча, оскільки гіпермаркет продає більше товарів, ніж рундуків.
Декілька слів про коректність вихідних даних, що використовуються для передбачення
Припустимо, ми маємо таблицю, побудовану за даними для n магазинів.
Відповідно до математичної статистики, результати будуть більш-менш коректними, якщо досліджуються дані з хоча б 5-6 об'єктів. Крім того, не можна використовувати "аномальні" результати. Зокрема, елітний невеликий бутік може мати товарообіг у рази більший, ніж товарообіг великих торгових точок класу «Масмаркет».
Суть методу
Дані таблиці можна зобразити на декартовій площині у вигляді точок M 1 (x 1 y 1), ... M n (x n y n). Тепер розв'язання задачі зведеться до підбору апроксимуючої функції y = f (x), що має графік, що проходить якомога ближче до точок M1, M2,.. Mn.
Звичайно, можна використовувати багаточлен високого ступеня, але такий варіант не тільки важко реалізувати, але й просто некоректний, тому що не відображатиме основну тенденцію, яку і потрібно виявити. Найрозумнішим рішенням є пошук прямої у = ax + b, яка найкраще наближає експериментальні дані, a точніше, коефіцієнтів – a та b.
Оцінка точності
При будь-якій апроксимації особливої важливості набуває оцінка її точності. Позначимо через e i різницю (відхилення) між функціональними та експериментальними значеннями для точки x i , тобто e i = y i - f (x i).
Очевидно, що для оцінки точності апроксимації можна використовувати суму відхилень, тобто при виборі прямої для наближеного уявлення залежності X від Y потрібно віддавати перевагу тій, у якої найменше значення суми e i у всіх точках. Однак, не все так просто, тому що поряд із позитивними відхиленнями практично будуть присутні і негативні.
Вирішити питання можна, використовуючи модулі відхилень або їх квадрати. Останній метод набув найбільш широкого поширення. Він використовується в багатьох областях, включаючи регресійний аналіз (в Excel його реалізація здійснюється за допомогою двох вбудованих функцій) і давно довів свою ефективність.
Метод найменших квадратів
В Excel, як відомо, існує вбудована функція автосуми, що дозволяє обчислити значення всіх значень, які розташовані у виділеному діапазоні. Таким чином, ніщо не завадить нам розрахувати значення виразу (e 1 2 + e 2 2 + e 3 2 + ... e n 2).
У математичному записі це має вигляд:

Оскільки спочатку було прийнято рішення про апроксимування за допомогою прямої, то маємо:

Таким чином, завдання знаходження прямої, яка найкраще описує конкретну залежність величин X та Y, зводиться до обчислення мінімуму функції двох змінних:

Для цього потрібно прирівняти до нуля приватні похідні за новими змінними a і b, і вирішити примітивну систему, що складається з двох рівнянь із двома невідомими видами:

Після нехитрих перетворень, включаючи поділ на 2 та маніпуляції із сумами, отримаємо:

Вирішуючи її, наприклад, методом Крамера, отримуємо стаціонарну точку з деякими коефіцієнтами a * та b *. Це і є мінімум, тобто для передбачення, який товарообіг буде у магазину при певній площі, підійде пряма y = a * x + b * , Що являє собою регресійну модель для прикладу, про який йдеться. Звичайно, вона не дозволить знайти точний результат, але допоможе одержати уявлення про те, чи окупиться покупка в кредит магазину конкретної площі.
Як реалізувати метод найменших квадратів в Excel
У "Ексель" є функція для розрахунку значення МНК. Вона має такий вигляд: «ТЕНДЕНЦІЯ» (відоме значення Y; відоме значення X; нові значення X; конст.). Застосуємо формулу розрахунку МНК Excel до нашої таблиці.
Для цього в комірку, в якій має бути відображено результат розрахунку за методом найменших квадратів в Excel, введемо знак = і виберемо функцію ТЕНДЕНЦІЯ. У вікні заповнимо відповідні поля, виділяючи:
- діапазон відомих значень для Y (у разі дані для товарообігу);
- діапазон x 1, … x n, тобто величини торгових площ;
- і відомі, і невідомі значення x, для якого потрібно з'ясувати розмір товарообігу (інформацію про їхнє розташування на робочому аркуші див. далі).
Крім того, у формулі є логічна змінна «Конст». Якщо ввести у відповідне їй поле 1, це означатиме, що слід здійснити обчислення, вважаючи, що b = 0.
Якщо потрібно дізнатися прогноз для більш ніж одного значення x, то після введення формули слід натиснути не на Введення, а потрібно набрати на клавіатурі комбінацію Shift + Control + Enter (Введення).
Деякі особливості
Регресійний аналіз може бути доступним навіть чайникам. Формула Excel для передбачення значення масиву невідомих змінних - "ТЕНДЕНЦІЯ" - може використовуватися навіть тими, хто ніколи не чув про метод найменших квадратів. Досить просто знати деякі особливості її роботи. Зокрема:
- Якщо розташувати діапазон відомих значень змінної y в одному рядку або стовпці, то кожен рядок (стовпець) з відомими значеннями x сприйматиметься програмою як окрема змінна.
- Якщо у вікні «ТЕНДЕНЦІЯ» не вказаний діапазон з відомими x, то у разі використання функції Excel програма буде розглядати його як масив, що складається з цілих чисел, кількість яких відповідає діапазону із заданими значеннями змінної y.
- Щоб отримати на виході масив "передбачених" значень, вираз для обчислення тенденції потрібно вводити як формулу масиву.
- Якщо не вказано нових значень x, то функція «ТЕНДЕНЦІЯ» вважає їх рівним відомим. Якщо вони не задані, то як аргумент береться масив 1; 2; 3; 4;…, який відповідає діапазону з вже заданими параметрами y.
- Діапазон, що містить нові значення x, повинен складатися з такої ж або більшої кількості рядків або стовпців, як діапазон із заданими значеннями y. Іншими словами він має бути пропорційним незалежним змінним.
- У масиві з відомими значеннями x може бути кілька змінних. Однак якщо йдеться лише про одну, то потрібно, щоб діапазони із заданими значеннями x та y були пропорційні. У разі кількох змінних потрібно, щоб діапазон із заданими значеннями y містився в одному стовпці або в одному рядку.

Функція «ПЕРЕДСКАЗ»
Реалізується за допомогою кількох функцій. Одна з них називається «Предказ». Вона аналогічна «ТЕНДЕНЦІЇ», тобто видає результат обчислень методом найменших квадратів. Однак лише для одного X, для якого невідомо значення Y.
Тепер ви знаєте формули Excel для чайників, що дозволяють спрогнозувати величину майбутнього значення того чи іншого показника згідно з лінійним трендом.
3. Апроксимація функцій за допомогою методу
найменших квадратів
Метод найменших квадратів застосовується при обробці результатів експерименту для апроксимації (Наближення) експериментальних даних аналітичною формулою. Конкретний вид формули вибирається, зазвичай, з фізичних міркувань. Такими формулами можуть бути:
![]()
![]()
та інші.
Сутність методу найменших квадратів ось у чому. Нехай результати вимірів представлені таблицею:
|
Таблиця 4 |
||||
|
x n |
||||
|
y n |
||||
|
(3.1) |
де f - відома функція, a 0 , a 1 , …, a m - невідомі постійні параметри, значення яких слід знайти. У методі найменших квадратів наближення функції (3.1) до експериментальної залежності вважається найкращим, якщо виконується умова
|
(3.2) |
тобто сум a квадратів відхилень шуканої аналітичної функції від експериментальної залежності має бути мінімальною .
Зауважимо, що функція Q називається нев'язкою.

Бо нев'язка

вона має мінімум. Необхідною умовою мінімуму функції кількох змінних є рівність нуля всіх приватних похідних цієї функції за параметрами. Таким чином, відшукання найкращих значень параметрів апроксимуючої функції (3.1), тобто таких значень, при яких Q = Q (a 0 , a 1 , …, a m ) мінімальна, зводиться до розв'язання системи рівнянь:
|
(3.3) |
Методу найменших квадратів можна дати таке геометричне тлумачення: серед нескінченного сімейства ліній цього виду знаходиться одна лінія, на яку сума квадратів різниць ординат експериментальних точок і відповідних їм ординат точок, знайдених за рівнянням цієї лінії, буде найменшою.
Знаходження параметрів лінійної функції
Нехай експериментальні дані треба подати лінійною функцією:
Потрібно підібрати такі значення a і b , для яких функція
|
(3.4) |
буде мінімальною. Необхідні умови мінімуму функції (3.4) зводяться до системи рівнянь:
|
|
Після перетворень отримуємо систему двох лінійних рівнянь із двома невідомими:
|
|
(3.5) |
вирішуючи яку , знаходимо шукані значення параметрів a і b.
Знаходження параметрів квадратичної функції
Якщо апроксимуючою функцією є квадратична залежність
то її параметри a, b, c знаходять із умови мінімуму функції:
|
(3.6) |
Умови мінімуму функції (3.6) зводяться до системи рівнянь:
|
|
Після перетворень отримуємо систему трьох лінійних рівнянь із трьома невідомими:
|
|
(3.7) |
при вирішенні якої знаходимо шукані значення параметрів a, b і c.
Приклад . Нехай у результаті експерименту отримано наступну таблицю значень x та y :
|
Таблиця 5 |
||||||||
|
y i |
0,705 |
0,495 |
0,426 |
0,357 |
0,368 |
0,406 |
0,549 |
0,768 |
Потрібно апроксимувати експериментальні дані лінійною та квадратичною функціями.
Рішення. Пошук параметрів апроксимуючих функцій зводиться до вирішення систем лінійних рівнянь (3.5) і (3.7). Для вирішення задачі скористаємося процесором електронних таблиць Excel.
1. Спочатку зчепимо листи 1 і 2. Занесемо експериментальні значення x i та y iу стовпці А і В, починаючи з другого рядка (у першому рядку помістимо заголовки стовпців). Потім для цих стовпців обчислимо суми та помістимо їх у десятому рядку.
У стовпцях C – G розмістимо відповідно обчислення та підсумовування
2. Розчепимо листи. Подальші обчислення проведемо аналогічним чином для лінійної залежності на аркуші 1і для квадратичної залежності на аркуші 2.
3. Під отриманою таблицею сформуємо матрицю коефіцієнтів та вектор-стовпець вільних членів. Розв'яжемо систему лінійних рівнянь за наступним алгоритмом:
Для обчислення зворотної матриці та перемноження матриць скористаємося Майстром функційта функціями МОБРі МУМНОЖ.
4. У блоці осередків H2: H 9 на основі отриманих коефіцієнтів обчислимо значення апроксимуючогополіномаy i вич., у блоці I 2: I 9 – відхилення D y i = y i експ. - y i вич., у стовпці J – нев'язку:
Отримані таблиці та побудовані за допомогою Майстри діаграмграфіки наведені на рисунках6, 7, 8.

Рис. 6. Таблиця обчислення коефіцієнтів лінійної функції,
апроксимуючоюекспериментальні дані.

Рис. 7. Таблиця обчислення коефіцієнтів квадратичної функції,
апроксимуючоюекспериментальні дані.

Рис. 8. Графічне подання результатів апроксимації
експериментальних даних лінійної та квадратичної функціями.
Відповідь. Апроксимували експериментальні дані лінійною залежністю y = 0,07881 x + 0,442262 з нев'язкою Q = 0,165167 та квадратичною залежністю y = 3,115476 x 2 – 5,2175 x + 2,529631 з нев'язкою Q = 0,002103 .
Завдання. Апроксимувати функцію, задану таблично, лінійною та квадратичною функціями.
|
Таблиця 6 |
|||||||||
|
№0 |
x |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
|
y |
3,030 |
3,142 |
3,358 |
3,463 |
3,772 |
3,251 |
3,170 |
3,665 |
|
|
№ 1 |
|||||||||
|
3,314 |
3,278 |
3,262 |
3,292 |
3,332 |
3,397 |
3,487 |
3,563 |
||
|
№ 2 |
|||||||||
|
1,045 |
1,162 |
1,264 |
1,172 |
1,070 |
0,898 |
0,656 |
0,344 |
||
|
№ 3 |
|||||||||
|
6,715 |
6,735 |
6,750 |
6,741 |
6,645 |
6,639 |
6,647 |
6,612 |
||
|
№ 4 |
|||||||||
|
2,325 |
2,515 |
2,638 |
2,700 |
2,696 |
2,626 |
2,491 |
2,291 |
||
|
№ 5 |
|||||||||
|
1.752 |
1,762 |
1,777 |
1,797 |
1,821 |
1,850 |
1,884 |
1,944 |
||
|
№ 6 |
|||||||||
|
1,924 |
1,710 |
1,525 |
1,370 |
1,264 |
1,190 |
1,148 |
1,127 |
||
|
№ 7 |
|||||||||
|
1,025 |
1,144 |
1,336 |
1,419 |
1,479 |
1,530 |
1,568 |
1,248 |
||
|
№ 8 |
|||||||||
|
5,785 |
5,685 |
5,605 |
5,545 |
5,505 |
5,480 |
5,495 |
5,510 |
||
|
№ 9 |
|||||||||
|
4,052 |
4,092 |
4,152 |
4,234 |
4,338 |
4,468 |
4,599 |
КУРСОВА РОБОТА Апроксимація функції методом найменших квадратів Вступ емпіричний mathcad апроксимація Метою курсової роботи є поглиблення знань з інформатики, розвиток та закріплення навичок роботи з табличним процесором Microsoft Excel та MathCAD. Застосування їх вирішення завдань з допомогою ЕОМ з предметної області, що з дослідженнями. У кожному завданні формулюються умови завдання, вихідні дані, форма видачі результатів, вказуються основні математичні залежності для вирішення задачі. Контрольний розрахунок дозволяє переконатися у правильності роботи програми. Поняття апроксимація є наближеним виразом будь-яких математичних об'єктів (наприклад, чисел або функцій) через інші більш прості, більш зручні у використанні або просто більш відомі. У наукових дослідженнях апроксимація застосовується для опису, аналізу, узагальнення та подальшого використання емпіричних результатів. Як відомо, між величинами може існувати точний (функціональний) зв'язок, коли одному значенню аргументу відповідає одне певне значення, і менш точний (кореляційний) зв'язок, коли одному конкретному значенню аргументу відповідає наближене значення або деяка множина значень функції, тією чи іншою мірою близьких один до одного. При веденні наукових досліджень, обробці результатів спостереження чи експерименту зазвичай доводиться стикатися з другим варіантом. При вивченні кількісних залежностей різних показників, значення яких визначаються емпірично, як правило, є деяка їхня варіабельність. Частково вона задається неоднорідністю самих об'єктів, що вивчаються, неживої і, особливо, живої природи, частково обумовлюється похибкою спостереження та кількісної обробки матеріалів. Останню складову який завжди вдається виключити повністю, можна лише мінімізувати її ретельним вибором адекватного методу дослідження та акуратністю роботи. Фахівці в галузі автоматизації технологічних процесів та виробництв мають справу з великим обсягом експериментальних даних, для обробки яких використовується комп'ютер. Вихідні дані та отримані результати обчислень можуть бути представлені в табличній формі, використовуючи табличні процесори (електронні таблиці) і, зокрема, Excel. Курсова робота з інформатики дозволяє студенту закріпити і розвинути навички роботи за допомогою базових комп'ютерних технологій при вирішенні завдань у сфері професійної діяльності. для колективної роботи 1. Загальні відомості Дуже часто, особливо при аналізі емпіричних даних, виникає необхідність знайти в явному вигляді функціональну залежність між величинами xі у, що отримані в результаті вимірювань. При аналітичному дослідженні взаємозв'язку між двома величинами x та y виробляють ряд спостережень і в результаті виходить таблиця значень: xx1 x1 xiXnуy1 y1 yiYn Ця таблиця зазвичай виходить як результат будь-яких експериментів, у яких x,(незалежна величина) задається експериментатором, а у,виходить у результаті досвіду. Тому ці значення у,називатимемо емпіричними або досвідченими значеннями. Між величинами x та y існує функціональна залежність, але її аналітичний вигляд зазвичай невідомий, тому виникає практично важливе завдання – знайти емпіричну формулу y =f (x; a 1, a 2,…, am ), (1) (де a1 , a2 ,…, am- параметри), значення якої при x = x,можливо мало відрізнялися б від досвідчених значень у, (i = 1,2,…, д). Зазвичай вказують клас функцій (наприклад, безліч лінійних, статечних, показових і т.п.), з якого вибирається функція f(x), і надалі визначаються найкращі значення параметрів. Якщо в емпіричну формулу (1) підставити вихідні x,то отримаємо теоретичні значення YTi= f (xi; a 1, a 2……am) , де i = 1,2,…, n. Різниці yiT- уi, називаються відхиленнями і є відстані по вертикалі від точок Miдо графіка емпіричної функції Згідно з методом найменших квадратів найкращими коефіцієнтами a1 , a2 ,…, amвважаються ті, для яких сума квадратів відхилень знайденої емпіричної функції від заданих значень функції буде мінімальною. Пояснимо геометричний зміст методу найменших квадратів. Кожна пара чисел ( xi, yi) з вихідної таблиці визначає точку Miна площині XOY.Використовуючи формулу (1) при різних значеннях коефіцієнтів a1 , a2 ,…, amможна побудувати низку кривих, які є графіками функції (1). Завдання полягає у визначенні коефіцієнтів a1 , a2 ,…, amтаким чином, щоб сума квадратів відстаней по вертикалі від точок Mi (xi, yi) до графіка функції (1) була найменшою (рис. 1). Побудова емпіричної формули складається з двох етапів: з'ясування загального виду цієї формули та визначення її найкращих параметрів. Якщо невідомий характер залежності між даними величинами x та y, то вид емпіричної залежності є довільним. Перевага надається простим формулам, що мають хорошу точність. Вдалий вибір емпіричної формули значною мірою залежить від знань дослідника у предметній області, використовуючи які може вказати клас функцій з теоретичних міркувань. Велике значення має зображення отриманих даних у декартових або спеціальних системах координат (напівлогарифмічної, логарифмічної тощо). По положенню точок можна приблизно вгадати загальний вигляд залежності шляхом встановлення подібності між побудованим графіком та зразками відомих кривих. Визначення найкращих коефіцієнтів a1 , a2,…, amщо входять до емпіричної формули виробляють добре відомим аналітичними методами. Для того, щоб знайти набір коефіцієнтів a1 , a2 …..am, які доставляють мінімум функції S, яка визначається формулою (2), використовуємо необхідну умову екстремуму функції кількох змінних - рівність нулю приватних похідних. В результаті отримаємо нормальну систему для визначення коефіцієнтів ai(i = 1,2,…, m): Таким чином, знаходження коефіцієнтів aiзводиться до вирішення системи (3). Ця система спрощується, якщо емпірична формула (1) лінійна щодо параметрів aiтоді система (3) - буде лінійною. 1.1 Лінійна залежність Конкретний вид системи (3) залежить від цього, з якого класу емпіричних формул ми шукаємо залежність (1). У разі лінійної залежності y = a1 + a2 xсистема (3) набуде вигляду: Ця лінійна система може бути вирішена будь-яким відомим методом (методом Гауса, найпростіших ітерацій, формулами Крамера). 1.2 Квадратична залежність У разі квадратичної залежності y = a1 + a2 x + a3x 2система (3) набуде вигляду: 1.3 Експонентна залежність У ряді випадків як емпірична формула беруть функцію в яку невизначені коефіцієнти входять нелінійно. У цьому іноді завдання вдається лінеаризувати тобто. звести до лінійної. До таких залежностей належить експоненційна залежність y = a1 * ea2x (6) де a 1і a 2, невизначені кофіцієнти Лінеаризація досягається шляхом логарифмування рівності (6), після чого отримуємо співвідношення ln y = ln a 1+a 2x (7) Позначимо ln ута ln axвідповідно через tі cтоді залежність (6) може бути записана у вигляді t = a1 + a2 х, що дозволяє застосувати формули (4) із заміною a1 на cі уiна ti 1.4 Елементи теорії кореляції Графік відновленої функціональної залежності у(х)за результатами вимірювань (х i, уi),i = 1,2, K, nназивається кривою регресії. Для перевірки згоди побудованої кривої регресії з результатами експерименту зазвичай запроваджують такі числові характеристики: коефіцієнт кореляції (лінійна залежність), кореляційне ставлення та коефіцієнт детермінованості. У цьому результати зазвичай групують і представляють формі кореляційної таблиці. У кожній клітині цієї таблиці наводяться чисельності niJ - тих пар (х, у), компоненти яких потрапляють у відповідні інтервали угруповання з кожної змінної. Припускаючи довжини інтервалів угруповання (по кожному змінному) рівними між собою, вибирають центри х i(відповідно уi) цих інтервалів та числа niJ- як основа для розрахунків. Коефіцієнт кореляції є мірою лінійного зв'язку між залежними випадковими величинами: він показує, наскільки добре в середньому може бути представлена одна з величин у вигляді лінійної функції від іншої. Коефіцієнт кореляції обчислюється за такою формулою: де, і - середнє арифметичне значення відповідно хі у. Коефіцієнт кореляції між випадковими величинами за абсолютною величиною вбирається у 1. Чим ближче |р| до 1, тим більше лінійний зв'язок між х і у. У разі нелінійного кореляційного зв'язку умовні середні значення розташовуються біля кривої лінії. І тут як характеристики сили зв'язку рекомендується використовувати кореляційне ставлення, інтерпретація якого залежить від виду досліджуваної залежності. Кореляційне відношення обчислюється за такою формулою: де ni = , nf= , а чисельник характеризує розсіювання умовних середніх у,біля середнього середнього y. Завжди. Рівність = 0 відповідає некорельованим випадковим величинам; = 1 тоді і тільки тоді, коли є точний функціональний зв'язок між yта x. У разі лінійної залежності yвід x кореляційне відношення збігається із квадратом коефіцієнта кореляції. Величина - ? 2 використовується як індикатор відхилення регресії від лінійної. Кореляційне відношення є мірою кореляційного зв'язку yз xв будь-якій формі, але не може дати уявлення про ступінь наближеності емпіричних даних до спеціальної форми. Щоб з'ясувати, наскільки точно побудована крива відображає емпіричні дані, вводиться ще одна характеристика - коефіцієнт детермінованості. Для його опису розглянемо такі величини. - Повна сума квадратів, де середнє значення. Можна довести таку рівність Перше доданок дорівнює Sост = і називається залишковою сумою квадратів. Воно характеризує відхилення експериментальних від теоритичних. Друге доданок дорівнює Sрегр = 2 і називається регресійною сумою квадратів і воно характеризує розкид даних. Очевидно, що справедлива наступна рівність S повний = S зуст + S регр. Коефіцієнт детермінованості визначається за такою формулою: Чим менша залишкова сума квадратів порівняно із загальною сумою квадратів, тим більше значення коефіцієнта детермінованості r2 , Який показує, наскільки добре рівняння, отримане за допомогою регресійного аналізу, пояснює взаємозв'язок між змінними. Якщо він дорівнює 1, має місце повна кореляція з моделлю, тобто. немає різниці між фактичним та оцінним значеннями y. У протилежному випадку, якщо коефіцієнт детермінованості дорівнює 0, то рівняння регресії невдало для передбачення значень y Коефіцієнт детермінованості завжди перевищує кореляційне ставлення. У разі коли виконується рівність r 2 = можна вважати, що побудована емпірична формула найбільш точно відображає емпіричні дані. 2. Постановка задачі 1. Використовуючи метод найменших квадратів функцію, задану таблично, апроксимувати а) багаточлен першого ступеня; б) багаточлен другого ступеня; в) експоненційною залежністю. Для кожної залежності вирахувати коефіцієнт детермінованості. Обчислити коефіцієнт кореляції (тільки у разі а). Для кожної залежності побудувати лінію тренду. Використовуючи функцію Лінейн обчислити числові характеристики в залежності від. Порівняти свої обчислення з результатами, отриманими за допомогою функції Лінейн. Зробити висновок, яка з отриманих формул якнайкраще апроксимує функцію. Написати програму однією з мов програмування та порівняти результати рахунку з отриманими вище. 3. Вихідні дані Функція задана малюнком 1. 4. Розрахунок апроксимацій у табличному процесорі Excel Для проведення розрахунків доцільно користуватися табличним процесором Microsoft Excel. І дані розмістити як показано малюнку 2. Для цього заносимо: · у комірки A6:A30 заносимо значення xi . · у комірки B6:B30 заносимо значення уi . · у комірку C6 вводимо формулу = А6 ^ 2. · у комірки C7:C30 ця формула копіюється. · у комірку D6 вводимо формулу = А6 * В6. · у комірки D7:D30 ця формула копіюється. · у комірку F6 вводимо формулу =А6^4. · у комірки F7:F30 ця формула копіюється. · у комірку G6 вводимо формулу =А6^2*В6. · у комірки G7:G30 ця формула копіюється. · у комірку H6 вводимо формулу =LN(B6). · у комірки H7:H30 ця формула копіюється. · у комірку I6 вводимо формулу =A6*LN(B6). · у комірки I7:I30 ця формула копіюється. Наступні кроки робимо за допомогою автосумування · в комірку А33 вводимо формулу = СУМ (А6: А30). · в комірку B33 вводимо формулу = СУМ (В6: В30). · в комірку C33 вводимо формулу = СУМ (С6: С30). · в комірку D33 вводимо формулу = СУМ (D6: D30). · у комірку E33 вводимо формулу = СУМ (E6: E30). · у комірку F33 вводимо формулу = СУМ (F6: F30). · в комірку G33 вводимо формулу = СУМ (G6: G30). · в комірку H33 вводимо формулу = СУМ (H6: H30). · в комірку I33 вводимо формулу = СУМ (I6: I30). Апроксимуємо функцію y = f(x) лінійною функцією y = a1 + a2x. Для визначення коефіцієнтів a 1та a 2скористаємося системою (4). Використовуючи підсумкові суми таблиці 2, розташовані в осередках A33, B33, C33 та D33, запишемо систему (4) у вигляді вирішивши яку, отримаємо a 1= -24,7164 та a2 = 11,63183 Таким чином, лінійна апроксимація має вигляд y=-24,7164 + 11,63183х (12) Рішення системи (11) проводили, використовуючи засоби Microsoft Excel. Результати представлені на малюнку 3: У таблиці в осередках A38: B39 записано формулу (= МОБР (A35: B36)). У осередках E38:E39 записана формула (=МУМНОЖ (A38:B39, C35:C36)). Далі апроксимуємо функцію y = f(x) квадратичною функцією y = a1 + a2 x + a3 x2. Для визначення коефіцієнтів a 1, a 2та a 3скористаємося системою (5). Використовуючи підсумкові суми таблиці 2, розташовані в осередках A33, B33, C33, D33, E33, F33 та G33 запишемо систему (5) у вигляді: Вирішивши яку, отримаємо a 1= 1,580946, a 2= -0,60819 та a3 = 0,954171 (14) Таким чином, квадратична апроксимація має вигляд: у = 1,580946-0,60819х +0,954171х2 Рішення системи (13) проводили, використовуючи засоби Microsoft Excel. Результати представлені малюнку 4. У таблиці в осередках A46: C48 записано формулу (=МОБР (A41: C43)). У осередках F46:F48 записана формула (=МУМНОЖ (A41:C43, D46:D48)). Тепер апроксимуємо функцію y = f(х) експоненційною функцією y = a1 ea2x. Для визначення коефіцієнтів a1 і a2 прологарифмуємо значення yiі використовуючи підсумкові суми таблиці 2, розташовані в осередках A26, C26, H26 та I26 отримаємо систему: де з = ln (a1 ). Вирішивши систему (10) знайдемо с =0,506435, a2 = 0.409819. Після потенціювання отримаємо a1 = 1,659365. Таким чином, експоненційна апроксимація має вигляд y = 1,659365 * e0,4098194x Рішення системи (15) проводили, використовуючи засоби Microsoft Excel. Результати представлені малюнку 5. У таблиці в осередках A55: B56 записано формулу (=МОБР (A51: B52)). У осередках E54:E56 записана формула (=МУМНОЖ (A51:B52, С51:С52)). У осередку E56 записана формула = EXP (E54). Обчислимо середнє арифметичне x і у за формулами: Результати розрахунку x та yзасобами Microsoft Excel представлені малюнку 6. У осередку B58 записано формулу =A33/25. У осередку B59 записано формулу =B33/25. Таблиця 2 Пояснимо як таблиця на рисунку 7 складається. Осередки A6:A33 і B6:B33 вже заповнені (див. мал. 2). · у комірку J6 вводимо формулу =(A6-$B$58)*(B6-$B$59). · у комірки J7:J30 ця формула копіюється. · у комірку K6 вводимо формулу =(А6-$В$58)^ 2. · у комірки K7:K30 ця формула копіюється. · у комірку L6 вводимо формулу =(В1-$В$59)^2. · у комірки L7:L30 ця формула копіюється. · у комірку M6 вводимо формулу =($Е$38+$Е$39*А6-В6)^2. · у комірки M7:M30 ця формула копіюється. · у комірку N6 вводимо формулу =($F$46 +$F$47*A6 +$F$48*A6 Л6-В6)^2. · у комірки N7:N30 ця формула копіюється. · у комірку O6 вводимо формулу =($Е$56*ЕХР ($Е$55*А6) - В6)^2. · у комірки O7:O30 ця формула копіюється. Наступні кроки робимо за допомогою автосумування. · у комірку J33 вводимо формулу = CYMM (J6: J30). · в комірку K33 вводимо формулу = СУМ (К6: К30). · у комірку L33 вводимо формулу = CYMM (L6: L30). · у комірку M33 вводимо формулу = СУМ (М6: М30). · у комірку N33 вводимо формулу = СУМ (N6: N30). · в комірку O33 вводимо формулу = СУМ (06:030). Тепер проведемо розрахунки коефіцієнта кореляції за формулою (8) (лише для лінійної апроксимації) та коефіцієнта детермінованості за формулою (10). Результати розрахунків засобами Microsoft Ехcеl представлені малюнку 7. У таблиці 8 у осередку B61 записана формула =J33/(K33*L33^(1/2). У осередку B62 записана формула =1 - M33/L33. У осередку B63 записана формула =1 - N33/L33. У осередку B64 записана Формула =1 - O33/L33. Аналіз результатів розрахунків показує, що квадратична апроксимація найкраще визначає експериментальні дані. 4.1 Побудова графіків у Excel Виділимо осередки A1: A25, після цього звернемося до майстра діаграм. Виберемо точковий графік. Після того як діаграма буде побудована, клацніть правою кнопкою мишки на лінії графіка і виберемо додати лінію тренда (відповідно лінійну, експоненційну, статечну та поліноміальну другого ступеня). Графік лінійної апроксимації Графік квадратичної апроксимації Графік експоненційної апроксимації. 5. Апроксимація функції за допомогою MathCAD Апроксимація даних з урахуванням їх статистичних параметрів відноситься до задач регресії. Вони зазвичай виникають при обробці експериментальних даних, отриманих в результаті вимірювань процесів або фізичних явищ, статистичних за своєю природою (як, наприклад, вимірювання радіометрії і ядерної геофізики), або на високому рівні перешкод (шумів). Завданням регресійного аналізу є підбір математичних формул, що найкраще описують експериментальні дані. .1 Лінійна регресія Лінійна регресія у системі Mathcad виконується за векторами аргументу Хта відліків Yфункціями: intercept (x, y)- обчислює параметр а1 , усунення лінії регресії по вертикалі (див. рис.) slope (x, y)- обчислює параметр a2 , кутовий коефіцієнт лінії регресії (див. мал.) y(x) = a1+a2*x Функція corr (у, y(x))обчислює коефіцієнт кореляції ПірсонаЧим він ближчий до 1, тим точніше оброблювані дані відповідають лінійній залежності (див. рис.) .2 Поліномінальна регресія Одновимірна поліноміальна регресія з довільним ступенем n полінома та з довільними координатами відліків у Mathcad виконується функціями: regress (х, у, n)- обчислює вектор S,у складі якого знаходяться коефіцієнти aiполінома n-й ступеня; Значення коефіцієнтів aiможуть бути витягнуті з вектора Sфункцією submatrix (S, 3, length(S) - 1, 0, 0). Отримані значення коефіцієнтів використовуємо у рівнянні регресії y(x) = a1+a2*x+a3*x2 (Див. мал.) .3 Нелінійна регресія Для простих типових формул апроксимації передбачено ряд функцій нелінійної регресії, у яких параметри функцій підбираються програмою Mathcad. До них належить функція expfit (x, y, s),яка повертає вектор, що містить коефіцієнти a1, a2і a3експоненційної функції y(x) = a1 ^exp (a2x) + a3.Вектор Sвводяться початкові значення коефіцієнтів a1, a2і a3першого наближення. Висновок Аналіз результатів розрахунків показує, що лінійна апроксимація найкраще визначає експериментальні дані. Результати, отримані за допомогою програми MathCAD, повністю збігаються зі значеннями, отриманими за допомогою Excel. Це говорить про вірність обчислень. Список використаної літератури
РепетиторствоПотрібна допомога з вивчення якоїсь теми?
Наші фахівці проконсультують або нададуть репетиторські послуги з цікавої для вас тематики. Апроксимація досвідчених даних - це метод, заснований на заміні експериментально отриманих даних аналітичною функцією, що найбільш близько проходить або збігається в вузлових точках з вихідними значеннями (даними отриманими в ході досвіду або експерименту). В даний час існує два способи визначення аналітичної функції: За допомогою побудови інтерполяційного багаточлена n-ступеня, що проходить безпосередньо через усі точкизаданого масиву даних. В даному випадку апроксимуюча функція подається у вигляді: інтерполяційного багаточлена у формі Лагранжа або інтерполяційного багаточлена у формі Ньютона. За допомогою побудови апроксимуючого багаточлена n-ступеня, який проходить в найближчій близькості від точокіз заданого масиву даних. Таким чином, апроксимуюча функція згладжує всі випадкові перешкоди (або похибки), які можуть виникати при виконанні експерименту: значення, що вимірюються в ході досвіду, залежать від випадкових факторів, які коливаються за своїми власними випадковими законами (похибки вимірювань або приладів, неточність або помилки досвіду). У разі апроксимуюча функція визначається методом найменших квадратів. Метод найменших квадратів(В англомовній літературі Ordinary Least Squares, OLS) – математичний метод, заснований на визначенні апроксимуючої функції, яка будується в найближчій близькості від точок із заданого масиву експериментальних даних. Близькість вихідної та апроксимуючої функції F(x) визначається числовим заходом, а саме: сума квадратів відхилень експериментальних даних від апроксимуючої кривої F(x) має бути найменшою. Апроксимуюча крива, побудована за методом найменших квадратів Метод найменших квадратів використовується: Аби вирішити перевизначених систем рівнянь, коли кількість рівнянь перевищує кількість невідомих; Для пошуку рішення у разі звичайних (не перевизначених) нелінійних систем рівнянь; Для апроксимації точкових значень деякою апроксимуючою функцією. Апроксимуюча функція методом найменших квадратів визначається з умови мінімуму суми квадратів відхилень розрахункової апроксимуючої функції від заданого масиву експериментальних даних. Цей критерій методу найменших квадратів записується у вигляді наступного виразу:
Значення розрахункової апроксимуючої функції у вузлових точках Заданий масив експериментальних даних у вузлових точках. Квадратичний критерій має низку "хороших" властивостей, таких, як диференційність, забезпечення єдиного розв'язання задачі апроксимації при поліноміальних апроксимуючих функціях. Залежно та умовами завдання апроксимуюча функція є многочлен ступеня m Ступінь апроксимуючої функції не залежить від числа вузлових точок, але її розмірність повинна бути завжди меншою за розмірність (кількість точок) заданого масиву експериментальних даних.
∙ Якщо ступінь апроксимуючої функції m=1, то ми апроксимуємо табличну функцію прямою лінією (лінійна регресія). ∙ Якщо ступінь апроксимуючої функції m=2, то ми апроксимуємо табличну функцію квадратичною параболою (квадратична апроксимація). ∙ Якщо ступінь апроксимуючої функції m=3, то ми апроксимуємо табличну функцію кубічною параболою (кубічна апроксимація). У випадку, коли потрібно побудувати апроксимуючий многочлен ступеня m для заданих табличних значень, умова мінімуму суми квадратів відхилень за всіма вузловими точками переписується так:
Кількість заданих табличних значень. Необхідною умовою існування мінімуму функції є рівність нуля її приватних похідних за невідомими змінними
Перетворимо отриману лінійну систему рівнянь: розкриємо дужки і перенесемо вільні доданки в праву частину виразу. В результаті отримана система лінійних виразів алгебри буде записуватися в наступному вигляді:
Дана система лінійних виразів алгебри може бути переписана в матричному вигляді:
В результаті було отримано систему лінійних рівнянь розмірністю m+1, що складається з m+1 невідомих. Дана система може бути вирішена за допомогою будь-якого методу розв'язання лінійних рівнянь алгебри (наприклад, методом Гауса). Через війну рішення знайдено невідомі параметри апроксимуючої функції, які забезпечують мінімальну суму квадратів відхилень апроксимуючої функції від вихідних даних, тобто. найкраще можливе квадратичне наближення. Слід пам'ятати, що при зміні навіть одного значення вихідних даних, всі коефіцієнти змінять свої значення, оскільки вони повністю визначаються вихідними даними. Апроксимація вихідних даних лінійною залежністю (лінійна регресія) Як приклад, розглянемо методику визначення апроксимуючої функції, яка задана у вигляді лінійної залежності. Відповідно до методу найменших квадратів умова мінімуму суми квадратів відхилень записується у такому вигляді: Координати вузлових точок таблиці; Невідомі коефіцієнти апроксимуючої функції, заданої у вигляді лінійної залежності. Необхідною умовою існування мінімуму функції є рівність нуля її приватних похідних за невідомими змінними. В результаті отримуємо таку систему рівнянь:
Перетворимо отриману лінійну систему рівнянь.
Вирішуємо отриману систему лінійних рівнянь. Коефіцієнти апроксимуючої функції в аналітичному вигляді визначаються таким чином (метод Крамера):
Дані коефіцієнти забезпечують побудову лінійної апроксимуючої функції відповідно до критерію мінімізації суми квадратів апроксимуючої функції від заданих табличних значень (експериментальні дані). Алгоритм реалізації методу найменших квадратів 1. Початкові дані: Задано масив експериментальних даних із кількістю вимірів N Задано ступінь апроксимуючого багаточлена (m) 2. Алгоритм обчислення: 2.1. Визначаються коефіцієнти для побудови системи рівнянь розмірністю
Коефіцієнти системи рівнянь (ліва частина рівняння)
Вільні члени системи лінійних рівнянь (права частина рівняння)
2.2. Формування системи лінійних рівнянь розмірністю.
2.3. Вирішення системи лінійних рівнянь з метою визначення невідомих коефіцієнтів апроксимуючого багаточлена ступеня m. 2.4.Визначення суми квадратів відхилень апроксимуючого багаточлена від вихідних значень по всіх вузлових точках
Знайдене значення суми квадратів відхилень є мінімально можливим. Апроксимація за допомогою інших функцій Слід зазначити, що при апроксимації вихідних даних відповідно до методу найменших квадратів як апроксимуючу функцію іноді використовують логарифмічну функцію, експоненційну функцію і статечну функцію. Логарифмічна апроксимація Розглянемо випадок, коли апроксимуюча функція задана логарифмічною функцією виду: | ||