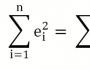Approssimazione dei dati sperimentali. Metodo dei minimi quadrati. Approssimazione di una funzione con il metodo dei minimi quadrati Utilizzo del metodo dei minimi quadrati per approssimare
Dopo l'allineamento, otteniamo una funzione della forma seguente: g (x) = x + 1 3 + 1 .
Possiamo approssimare questi dati con una relazione lineare y = a x + b calcolando i parametri appropriati. Per fare ciò, dovremo applicare il cosiddetto metodo dei minimi quadrati. Dovrai anche fare un disegno per verificare quale linea allineerà meglio i dati sperimentali.
Che cos'è esattamente OLS (metodo dei minimi quadrati)
La cosa principale che dobbiamo fare è trovare tali coefficienti di dipendenza lineare a cui il valore della funzione di due variabili F (a, b) = ∑ i = 1 n (yi - (axi + b)) 2 sarà il più piccolo . In altre parole, per determinati valori di aeb, la somma delle deviazioni al quadrato dei dati presentati dalla retta risultante avrà un valore minimo. Questo è il significato del metodo dei minimi quadrati. Tutto quello che dobbiamo fare per risolvere l'esempio è trovare l'estremo della funzione di due variabili.
Come ricavare formule per il calcolo dei coefficienti
Per ricavare formule per il calcolo dei coefficienti, è necessario comporre e risolvere un sistema di equazioni con due variabili. Per fare ciò, calcoliamo le derivate parziali dell'espressione F (a , b) = ∑ i = 1 n (y i - (a x i + b)) 2 rispetto ad aeb e le uguagliamo a 0 .
δ F (a , b) δ a = 0 δ F (a , b) δ b = 0 ⇔ - 2 ∑ io = 1 n (yi - (asse + b)) xi = 0 - 2 ∑ io = 1 n ( yi - (axi + b)) = 0 ⇔ a ∑ i = 1 nxi 2 + b ∑ i = 1 nxi = ∑ i = 1 nxiyia ∑ i = 1 nxi + ∑ i = 1 nb = ∑ i = 1 nyi ⇔ a ∑ i = 1 nxi 2 + b ∑ i = 1 nxi = ∑ i = 1 nxiyia ∑ i = 1 nxi + nb = ∑ i = 1 nyi
Per risolvere un sistema di equazioni, puoi utilizzare qualsiasi metodo, come la sostituzione o il metodo di Cramer. Di conseguenza, dovremmo ottenere formule che calcolano i coefficienti utilizzando il metodo dei minimi quadrati.
n ∑ io = 1 n x io y io - ∑ io = 1 n x io ∑ io = 1 n y io n ∑ io = 1 n - ∑ io = 1 n x io 2 b = ∑ io = 1 n y io - un ∑ io = 1 n x io n
Abbiamo calcolato i valori delle variabili per le quali la funzione
F (a , b) = ∑ i = 1 n (y i - (a x i + b)) 2 assumerà il valore minimo. Nel terzo paragrafo dimostreremo perché è così.
Questa è l'applicazione pratica del metodo dei minimi quadrati. La sua formula, che viene utilizzata per trovare il parametro a , include ∑ i = 1 n x i , ∑ i = 1 n y i , ∑ i = 1 n x i y i , ∑ i = 1 n x i 2 e il parametro
n - indica la quantità di dati sperimentali. Ti consigliamo di calcolare ogni importo separatamente. Il valore del coefficiente b viene calcolato immediatamente dopo a .
Torniamo all'esempio originale.
Esempio 1
Qui abbiamo n uguale a cinque. Per rendere più conveniente calcolare gli importi richiesti inclusi nelle formule dei coefficienti, compiliamo la tabella.
| io = 1 | io = 2 | io = 3 | io = 4 | io = 5 | ∑ io = 1 5 | |
| x io | 0 | 1 | 2 | 4 | 5 | 12 |
| si io | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 | 12 , 9 |
| x io e io | 0 | 2 , 4 | 5 , 2 | 11 , 2 | 15 | 33 , 8 |
| x io 2 | 0 | 1 | 4 | 16 | 25 | 46 |
Soluzione
La quarta riga contiene i dati ottenuti moltiplicando i valori della seconda riga per i valori della terza per ogni individuo i. La quinta riga contiene i dati del secondo quadrato. L'ultima colonna mostra le somme dei valori delle singole righe.
Usiamo il metodo dei minimi quadrati per calcolare i coefficienti aeb di cui abbiamo bisogno. Per fare ciò, sostituisci i valori desiderati dall'ultima colonna e calcola le somme:
n ∑ i = 1 nxiyi - ∑ i = 1 nxi ∑ i = 1 nyin ∑ i = 1 n - ∑ i = 1 nxi 2 b = ∑ i = 1 nyi - a ∑ i = 1 nxin ⇒ a = 5 33 , 8 - 12 12, 9 5 46 - 12 2 b = 12, 9 - a 12 5 ⇒ a ≈ 0, 165 b ≈ 2, 184
Abbiamo ottenuto che la retta approssimata desiderata sarà simile a y = 0, 165 x + 2, 184. Ora dobbiamo determinare quale linea approssima meglio i dati - g (x) = x + 1 3 + 1 o 0 , 165 x + 2 , 184 . Facciamo una stima usando il metodo dei minimi quadrati.
Per calcolare l'errore, dobbiamo trovare la somma delle deviazioni al quadrato dei dati dalle rette σ 1 = ∑ i = 1 n (yi - (axi + bi)) 2 e σ 2 = ∑ i = 1 n (yi - g (xi)) 2 , il valore minimo corrisponderà ad una linea più opportuna.
σ 1 = ∑ i = 1 n (yi - (asse + bi)) 2 = = ∑ i = 1 5 (yi - (0 , 165 xi + 2 , 184)) 2 ≈ 0 , 019 σ 2 = ∑ i = 1 n (yi - g (xi)) 2 = = ∑ io = 1 5 (yi - (xi + 1 3 + 1)) 2 ≈ 0 , 096
Risposta: poiché σ 1< σ 2 , то прямой, наилучшим образом аппроксимирующей исходные данные, будет
y = 0 , 165 x + 2 , 184 .
Il metodo dei minimi quadrati è mostrato chiaramente nell'illustrazione grafica. La linea rossa indica la retta g (x) = x + 1 3 + 1, la linea blu indica y = 0, 165 x + 2, 184. I dati grezzi sono contrassegnati da punti rosa.
Spieghiamo perché sono necessarie esattamente approssimazioni di questo tipo.
Possono essere utilizzati in problemi che richiedono il livellamento dei dati, nonché in quelli in cui i dati devono essere interpolati o estrapolati. Ad esempio, nel problema discusso sopra, si potrebbe trovare il valore della quantità osservata y in x = 3 o in x = 6 . Abbiamo dedicato un articolo separato a tali esempi.
Dimostrazione del metodo LSM
Perché la funzione assuma il valore minimo per aeb calcolati, è necessario che in un dato punto la matrice della forma quadratica del differenziale della funzione della forma F (a, b) = ∑ i = 1 n ( yi - (axi + b)) 2 essere definito positivo. Ti mostriamo come dovrebbe apparire.
Esempio 2
Abbiamo un differenziale del secondo ordine della seguente forma:
d 2 F (a ; b) = δ 2 F (a ; b) δ un 2 d 2 un + 2 δ 2 F (a ; b) δ un δ bdadb + δ 2 F (a ; b) δ b 2 d 2b
Soluzione
δ 2 F (a ; b) δ un 2 = δ δ F (a ; b) δ un δ un = = δ - 2 ∑ io = 1 n (yi - (asse + b)) xi δ un = 2 ∑ io = 1 n (xi) 2 δ 2 F (a ; b) δ un δ b = δ δ F (a ; b) δ un δ b = = δ - 2 ∑ io = 1 n (yi - (axi + b) ) xi δ b = 2 ∑ io = 1 nxi δ 2 F (a ; b) δ b 2 = δ δ F (a ; b) δ b δ b = δ - 2 ∑ io = 1 n (yi - (axi + b)) δ b = 2 ∑ io = 1 n (1) = 2 n
In altre parole, può essere scritto come segue: d 2 F (a ; b) = 2 ∑ i = 1 n (x i) 2 d 2 a + 2 2 ∑ x io io = 1 n d a d b + (2 n) d 2 b .
Abbiamo ottenuto una matrice di forma quadratica M = 2 ∑ i = 1 n (x i) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n .
In questo caso, i valori dei singoli elementi non cambieranno a seconda di aeb . Questa matrice è definita positiva? Per rispondere a questa domanda, controlliamo se i suoi minori angolari sono positivi.
Calcola l'angolo minore del primo ordine: 2 ∑ i = 1 n (x i) 2 > 0 . Poiché i punti x i non coincidono, la disuguaglianza è stretta. Lo terremo presente in ulteriori calcoli.
Calcoliamo il minore angolare del secondo ordine:
d e t (M) = 2 ∑ io = 1 n (x io) 2 2 ∑ io = 1 n x io 2 ∑ io = 1 n x io 2 n = 4 n ∑ io = 1 n (x io) 2 - ∑ io = 1 n x io 2
Successivamente, si procede alla dimostrazione della disuguaglianza n ∑ i = 1 n (x i) 2 - ∑ i = 1 n x i 2 > 0 utilizzando l'induzione matematica.
- Verifichiamo se questa disuguaglianza è valida per n arbitrario. Prendiamo 2 e calcoliamo:
2 ∑ io = 1 2 (xi) 2 - ∑ io = 1 2 xi 2 = 2 x 1 2 + x 2 2 - x 1 + x 2 2 = = x 1 2 - 2 x 1 x 2 + x 2 2 = x 1 + x 2 2 > 0
Abbiamo ottenuto l'uguaglianza corretta (se i valori x 1 e x 2 non corrispondono).
- Assumiamo che questa disuguaglianza sia vera per n , cioè n ∑ io = 1 n (x io) 2 - ∑ io = 1 n x io 2 > 0 – vero.
- Ora dimostriamo la validità per n + 1 , cioè che (n + 1) ∑ io = 1 n + 1 (xi) 2 - ∑ io = 1 n + 1 xi 2 > 0 se n ∑ io = 1 n (xi) 2 - ∑ io = 1 nxi 2 > 0 .
Calcoliamo:
(n + 1) ∑ io = 1 n + 1 (xi) 2 - ∑ io = 1 n + 1 xi 2 = = (n + 1) ∑ io = 1 n (xi) 2 + xn + 1 2 - ∑ io = 1 nxi + xn + 1 2 = = n ∑ i = 1 n (xi) 2 + n xn + 1 2 + ∑ i = 1 n (xi) 2 + xn + 1 2 - - ∑ i = 1 nxi 2 + 2 xn + 1 ∑ i = 1 nxi + xn + 1 2 = = ∑ i = 1 n (xi) 2 - ∑ i = 1 nxi 2 + n xn + 1 2 - xn + 1 ∑ i = 1 nxi + ∑ i = 1 n (xi) 2 = = ∑ io = 1 n (xi) 2 - ∑ io = 1 nxi 2 + xn + 1 2 - 2 xn + 1 x 1 + x 1 2 + + xn + 1 2 - 2 xn + 1 x 2 + x 2 2 + . . . + xn + 1 2 - 2 xn + 1 x 1 + xn 2 = = n ∑ i = 1 n (xi) 2 - ∑ i = 1 nxi 2 + + (xn + 1 - x 1) 2 + (xn + 1 - x 2) 2 + . . . + (x n - 1 - x n) 2 > 0
L'espressione racchiusa tra parentesi graffe sarà maggiore di 0 (in base a quanto ipotizzato nel passaggio 2) e il resto dei termini sarà maggiore di 0 perché sono tutti quadrati di numeri. Abbiamo dimostrato la disuguaglianza.
Risposta: gli aeb trovati corrisponderanno al valore più piccolo della funzione F (a, b) = ∑ i = 1 n (yi - (axi + b)) 2, il che significa che sono i parametri desiderati del metodo dei minimi quadrati (LSM).
Se noti un errore nel testo, evidenzialo e premi Ctrl+Invio
Ha molte applicazioni, in quanto consente una rappresentazione approssimativa di una data funzione con altre più semplici. LSM può essere estremamente utile nell'elaborazione delle osservazioni e viene utilizzato attivamente per stimare alcune quantità dai risultati di misurazioni di altre contenenti errori casuali. In questo articolo imparerai come implementare i calcoli dei minimi quadrati in Excel.
Espressione del problema su un esempio specifico
Supponiamo che ci siano due indicatori X e Y. Inoltre, Y dipende da X. Poiché OLS ci interessa dal punto di vista dell'analisi di regressione (in Excel, i suoi metodi sono implementati utilizzando funzioni integrate), dovremmo procedere immediatamente considerare un problema specifico.
Quindi, sia X l'area di vendita di un negozio di alimentari, misurata in metri quadrati, e Y il fatturato annuo, definito in milioni di rubli.
È necessario fare una previsione di quale fatturato (Y) avrà il negozio se ha una o un'altra area di vendita. Ovviamente la funzione Y = f (X) è crescente, poiché l'ipermercato vende più merce della bancarella.
Qualche parola sulla correttezza dei dati iniziali utilizzati per la previsione
Supponiamo di avere una tabella creata con i dati per n negozi.
Secondo la statistica matematica, i risultati saranno più o meno corretti se vengono esaminati i dati su almeno 5-6 oggetti. Inoltre, non è possibile utilizzare risultati "anomali". In particolare, una piccola boutique d'élite può avere un fatturato molte volte superiore a quello dei grandi outlet della classe “masmarket”.
L'essenza del metodo
I dati della tabella possono essere visualizzati sul piano cartesiano come punti M 1 (x 1, y 1), ... M n (x n, y n). Ora la soluzione del problema si riduce alla selezione di una funzione di approssimazione y = f (x), che ha un grafico passante il più vicino possibile ai punti M 1, M 2, .. M n .
Certo, puoi usare un polinomio di alto grado, ma questa opzione non è solo difficile da implementare, ma semplicemente errata, poiché non rifletterà la tendenza principale che deve essere rilevata. La soluzione più ragionevole è trovare la retta y = ax + b, che meglio approssima i dati sperimentali, o meglio, i coefficienti - aeb.
Punteggio di precisione
Per ogni approssimazione, la valutazione della sua accuratezza è di particolare importanza. Indichiamo con e i la differenza (deviazione) tra i valori funzionali e sperimentali per il punto x i , cioè e i = y i - f (x i).
Ovviamente per valutare l'accuratezza dell'approssimazione si può utilizzare la somma degli scostamenti, ovvero quando si sceglie una retta per una rappresentazione approssimativa della dipendenza di X da Y, si dovrebbe dare la preferenza a quella che ha il valore più piccolo della somma ei in tutti i punti in esame. Tuttavia, non tutto è così semplice, poiché insieme alle deviazioni positive ce ne saranno praticamente di negative.
Puoi risolvere il problema usando i moduli di deviazione o i loro quadrati. Quest'ultimo metodo è il più utilizzato. Viene utilizzato in molte aree, inclusa l'analisi di regressione (in Excel, la sua implementazione viene eseguita utilizzando due funzioni integrate) e da tempo si è dimostrato efficace.
Metodo dei minimi quadrati
In Excel, come sai, è presente una funzione di somma automatica incorporata che ti consente di calcolare i valori di tutti i valori situati nell'intervallo selezionato. Quindi nulla ci impedirà di calcolare il valore dell'espressione (e 1 2 + e 2 2 + e 3 2 + ... e n 2).
In notazione matematica, questo è simile a:

Poiché inizialmente è stata presa la decisione di approssimare utilizzando una retta, abbiamo:

Pertanto, il compito di trovare una retta che meglio descriva una specifica relazione tra X e Y equivale a calcolare il minimo di una funzione di due variabili:

Ciò richiede l'uguaglianza di derivate parziali zero rispetto alle nuove variabili aeb e la risoluzione di un sistema primitivo costituito da due equazioni con 2 incognite della forma:

Dopo semplici trasformazioni, inclusa la divisione per 2 e la manipolazione delle somme, otteniamo:

Risolvendolo, ad esempio, con il metodo di Cramer, otteniamo un punto stazionario con determinati coefficienti a * e b * . Questo è il minimo, cioè per prevedere quale fatturato avrà il negozio per una determinata area, è adatta la retta y = a * x + b *, che è un modello di regressione per l'esempio in questione. Certo, non ti permetterà di trovare il risultato esatto, ma aiuterà a farti un'idea se l'acquisto di un negozio a credito per una determinata area ripagherà.
Come implementare il metodo dei minimi quadrati in Excel
Excel ha una funzione per calcolare il valore dei minimi quadrati. Ha la forma seguente: TREND (valori Y noti; valori X noti; nuovi valori X; costante). Applichiamo la formula per il calcolo dell'OLS in Excel alla nostra tabella.
Per fare ciò, nella cella in cui deve essere visualizzato il risultato del calcolo con il metodo dei minimi quadrati in Excel, inserire il segno "=" e selezionare la funzione "TENDENZA". Nella finestra che si apre, compila gli appositi campi evidenziando:
- range di valori noti per Y (in questo caso dati per fatturato);
- intervallo x 1 , …x n , ovvero la dimensione dello spazio di vendita al dettaglio;
- e valori noti e sconosciuti di x, per i quali è necessario scoprire l'entità del fatturato (per informazioni sulla loro posizione nel foglio di lavoro, vedere sotto).
Inoltre, nella formula è presente una variabile logica "Const". Se inserisci 1 nel campo corrispondente, significa che è necessario eseguire i calcoli, supponendo che b \u003d 0.
Se hai bisogno di conoscere la previsione per più di un valore x, dopo aver inserito la formula, non dovresti premere "Invio", ma devi digitare la combinazione "Maiusc" + "Controllo" + "Invio" ("Invio" ) sulla tastiera.
Alcune caratteristiche
L'analisi di regressione può essere accessibile anche ai manichini. La formula di Excel per prevedere il valore di un array di variabili sconosciute - "TREND" - può essere utilizzata anche da coloro che non hanno mai sentito parlare del metodo dei minimi quadrati. Basta conoscere alcune caratteristiche del suo lavoro. In particolare:
- Se organizzi l'intervallo di valori noti della variabile y in una riga o colonna, ogni riga (colonna) con valori noti di x sarà percepita dal programma come una variabile separata.
- Se l'intervallo con x noto non è specificato nella finestra TENDENZA, nel caso di utilizzo della funzione in Excel, il programma lo considererà come un array composto da numeri interi, il cui numero corrisponde all'intervallo con i valori indicati della variabile y.
- Per emettere una matrice di valori "previsti", l'espressione di tendenza deve essere inserita come formula di matrice.
- Se non vengono specificati nuovi valori x, la funzione TREND li considera uguali a quelli noti. Se non sono specificati, l'array 1 viene preso come argomento; 2; 3; 4;…, che è commisurato all'intervallo con i parametri già dati y.
- L'intervallo contenente i nuovi valori x deve avere le stesse o più righe o colonne dell'intervallo con i valori y indicati. In altre parole, deve essere proporzionato alle variabili indipendenti.
- Un array con valori x noti può contenere più variabili. Tuttavia, se stiamo parlando di uno solo, è necessario che gli intervalli con i valori indicati di xey siano commisurati. Nel caso di più variabili, è necessario che l'intervallo con i valori y dati rientri in una colonna o in una riga.

funzione PREVISIONE
È implementato utilizzando diverse funzioni. Uno di questi si chiama "PREDIZIONE". È simile a TREND, ovvero fornisce il risultato di calcoli utilizzando il metodo dei minimi quadrati. Tuttavia, solo per una X, per la quale il valore di Y è sconosciuto.
Ora conosci le formule di Excel per i manichini che ti consentono di prevedere il valore del valore futuro di un indicatore secondo un andamento lineare.
3. Approssimazione di funzioni usando il metodo
minimi quadrati
Il metodo dei minimi quadrati viene utilizzato durante l'elaborazione dei risultati dell'esperimento per approssimazioni (approssimazioni) dati sperimentali formula analitica. La forma specifica della formula è scelta, di regola, da considerazioni fisiche. Queste formule possono essere:
![]()
![]()
e altri.
L'essenza del metodo dei minimi quadrati è la seguente. Lascia che i risultati della misurazione siano presentati nella tabella:
|
tavolo 4 |
||||
|
x n |
||||
|
si n |
||||
|
(3.1) |
dove f è una funzione nota, a 0 , a 1 , …, a m - parametri costanti sconosciuti, i cui valori devono essere trovati. Nel metodo dei minimi quadrati, l'approssimazione della funzione (3.1) alla dipendenza sperimentale è considerata la migliore se la condizione
|
(3.2) |
cioè importi un le deviazioni al quadrato della funzione analitica desiderata dalla dipendenza sperimentale dovrebbero essere minime .
Si noti che la funzione Q chiamata invisibile.

Dal momento che la discrepanza

allora ha un minimo. Condizione necessaria per il minimo di una funzione di più variabili è l'uguaglianza a zero di tutte le derivate parziali di questa funzione rispetto ai parametri. Quindi, trovando i migliori valori dei parametri della funzione di approssimazione (3.1), cioè quei valori per i quali Q = Q (a 0 , a 1 , …, a m ) è minimo, si riduce a risolvere il sistema di equazioni:
|
(3.3) |
Al metodo dei minimi quadrati si può dare la seguente interpretazione geometrica: tra una famiglia infinita di rette di un dato tipo si trova una retta per la quale la somma delle differenze al quadrato nelle ordinate dei punti sperimentali e le corrispondenti ordinate dei punti trovato dall'equazione di questa linea sarà il più piccolo.
Trovare i parametri di una funzione lineare
Lascia che i dati sperimentali siano rappresentati da una funzione lineare:
È necessario scegliere tali valori a e b , per cui la funzione
|
(3.4) |
sarà minimo. Le condizioni necessarie per il minimo della funzione (3.4) si riducono al sistema di equazioni:
|
|
Dopo le trasformazioni, otteniamo un sistema di due equazioni lineari con due incognite:
|
|
(3.5) |
risolvendo il quale, troviamo i valori desiderati dei parametri aeb.
Trovare i parametri di una funzione quadratica
Se la funzione di approssimazione è una dipendenza quadratica
quindi i suoi parametri a, b, c trovare dalla condizione minima della funzione:
|
(3.6) |
Le condizioni minime per la funzione (3.6) sono ridotte al sistema di equazioni:
|
|
Dopo le trasformazioni, otteniamo un sistema di tre equazioni lineari con tre incognite:
|
|
(3.7) |
a risolvendo il quale troviamo i valori desiderati dei parametri a, b e c.
Esempio . Lascia che la seguente tabella di valori sia ottenuta come risultato dell'esperimento x e y :
|
tavolo 5 |
||||||||
|
si io |
0,705 |
0,495 |
0,426 |
0,357 |
0,368 |
0,406 |
0,549 |
0,768 |
È necessario approssimare i dati sperimentali mediante funzioni lineari e quadratiche.
Soluzione. Trovare i parametri delle funzioni approssimanti si riduce a risolvere sistemi di equazioni lineari (3.5) e (3.7). Per risolvere il problema, utilizziamo un elaboratore di fogli di calcolo eccellere.
1. Per prima cosa colleghiamo i fogli 1 e 2. Inserisci i valori sperimentali x io e si io in colonne A e B, a partire dalla seconda riga (nella prima riga mettiamo le intestazioni delle colonne). Quindi calcoliamo le somme per queste colonne e le mettiamo nella decima riga.
Nelle colonne C–G posizionare rispettivamente il calcolo e la somma
2. Sganciare i fogli Ulteriori calcoli verranno eseguiti in modo simile per la dipendenza lineare dal Foglio 1 e per la dipendenza quadratica dal Foglio 2.
3. Nella tabella risultante, formiamo una matrice di coefficienti e un vettore colonna di termini liberi. Risolviamo il sistema di equazioni lineari secondo il seguente algoritmo:
Per calcolare la matrice inversa e moltiplicare le matrici, utilizziamo Maestro funzioni e funzioni MOBR e MUMNOZH.
4. Nel blocco di celle H2: h 9 in base ai coefficienti ottenuti, calcoliamo valori di approssimazione polinomiosi io cal., nel blocco I 2: I 9 - deviazioni D e io = si io esp. - si io cal., nella colonna J - la discrepanza:
Tabelle ottenute e costruite utilizzando Maghi grafici i grafici sono mostrati nelle figure 6, 7, 8.

Riso. 6. Tabella per il calcolo dei coefficienti di una funzione lineare,
approssimativo dati sperimentali.

Riso. 7. Tabella per il calcolo dei coefficienti di una funzione quadratica,
approssimativodati sperimentali.

Riso. 8. Rappresentazione grafica dei risultati dell'approssimazione
dati sperimentali funzioni lineari e quadratiche.
Risposta. I dati sperimentali sono stati approssimati dalla dipendenza lineare y = 0,07881 X + 0,442262 con residuo Q = 0,165167 e dipendenza quadratica y = 3,115476 X 2 – 5,2175 X + 2,529631 con residuo Q = 0,002103 .
Compiti. Approssima la funzione data dalle funzioni tabulari, lineari e quadratiche.
|
Tabella 6 |
|||||||||
|
№0 |
X |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
|
y |
3,030 |
3,142 |
3,358 |
3,463 |
3,772 |
3,251 |
3,170 |
3,665 |
|
|
№ 1 |
|||||||||
|
3,314 |
3,278 |
3,262 |
3,292 |
3,332 |
3,397 |
3,487 |
3,563 |
||
|
№ 2 |
|||||||||
|
1,045 |
1,162 |
1,264 |
1,172 |
1,070 |
0,898 |
0,656 |
0,344 |
||
|
№ 3 |
|||||||||
|
6,715 |
6,735 |
6,750 |
6,741 |
6,645 |
6,639 |
6,647 |
6,612 |
||
|
№ 4 |
|||||||||
|
2,325 |
2,515 |
2,638 |
2,700 |
2,696 |
2,626 |
2,491 |
2,291 |
||
|
№ 5 |
|||||||||
|
1.752 |
1,762 |
1,777 |
1,797 |
1,821 |
1,850 |
1,884 |
1,944 |
||
|
№ 6 |
|||||||||
|
1,924 |
1,710 |
1,525 |
1,370 |
1,264 |
1,190 |
1,148 |
1,127 |
||
|
№ 7 |
|||||||||
|
1,025 |
1,144 |
1,336 |
1,419 |
1,479 |
1,530 |
1,568 |
1,248 |
||
|
№ 8 |
|||||||||
|
5,785 |
5,685 |
5,605 |
5,545 |
5,505 |
5,480 |
5,495 |
5,510 |
||
|
№ 9 |
|||||||||
|
4,052 |
4,092 |
4,152 |
4,234 |
4,338 |
4,468 |
4,599 |
CORSO DI LAVORO Approssimazione di una funzione con il metodo dei minimi quadrati introduzione approssimazione empirica di mathcad Lo scopo del lavoro del corso è approfondire la conoscenza dell'informatica, sviluppare e consolidare le competenze nell'utilizzo del foglio di calcolo Microsoft Excel e MathCAD. La loro applicazione per risolvere problemi con l'aiuto di un computer dall'area disciplinare relativa alla ricerca. In ogni attività vengono formulate le condizioni del problema, i dati iniziali, il modulo per l'emissione dei risultati, vengono indicate le principali dipendenze matematiche per la risoluzione del problema Il calcolo del controllo consente di verificare il corretto funzionamento del programma. Il concetto di approssimazione è un'espressione approssimativa di alcuni oggetti matematici (ad esempio numeri o funzioni) attraverso altri più semplici, più convenienti da usare o semplicemente più noti. Nella ricerca scientifica, l'approssimazione viene utilizzata per descrivere, analizzare, generalizzare e utilizzare ulteriormente i risultati empirici. Come è noto, può esistere una connessione esatta (funzionale) tra i valori, quando un valore dell'argomento corrisponde a un valore specifico, e una connessione meno accurata (correlazione), quando un valore specifico dell'argomento corrisponde a un valore approssimativo o qualche insieme di valori di funzione più o meno vicini tra loro. Quando si conduce una ricerca scientifica, si elaborano i risultati di un'osservazione o di un esperimento, di solito si deve fare i conti con la seconda opzione. Quando si studiano le dipendenze quantitative di vari indicatori, i cui valori sono determinati empiricamente, di norma vi è una certa variabilità. È in parte determinato dall'eterogeneità degli oggetti studiati della natura inanimata e, soprattutto, vivente, in parte a causa dell'errore di osservazione e di elaborazione quantitativa dei materiali. Non sempre è possibile eliminare completamente l'ultimo componente, che può essere ridotto al minimo solo con un'oculata scelta di un metodo di ricerca adeguato e accuratezza di lavoro. Gli specialisti nel campo dell'automazione dei processi tecnologici e delle produzioni si occupano di una grande quantità di dati sperimentali, per l'elaborazione dei quali viene utilizzato un computer. I dati iniziali ei risultati dei calcoli ottenuti possono essere presentati in forma tabellare utilizzando elaboratori di fogli di calcolo (fogli di calcolo) e, in particolare, Excel. Il corso in informatica consente allo studente di consolidare e sviluppare capacità di lavoro con l'ausilio delle tecnologie informatiche di base nella risoluzione di problemi nell'ambito dell'attività professionale - un sistema di algebra informatica della classe dei sistemi di progettazione assistita da computer, incentrato sulla preparazione di documenti interattivi con calcoli e supporto visivo, è facile da usare e applicare per il lavoro di squadra. 1. Informazione Generale Molto spesso, soprattutto quando si analizzano dati empirici, diventa necessario trovare in modo esplicito la relazione funzionale tra le grandezze Xe a, che si ottengono a seguito di misurazioni. In uno studio analitico della relazione tra due quantità x e y, viene fatta una serie di osservazioni e il risultato è una tabella di valori: xx1 X1 XioXnsi1 y1 yioYn Questa tabella è solitamente ottenuta a seguito di alcuni esperimenti in cui X,(valore indipendente) è impostato dallo sperimentatore, e si,ottenuto grazie all'esperienza. Pertanto, questi valori si,saranno chiamati valori empirici o sperimentali. Esiste una relazione funzionale tra i valori xey, ma la sua forma analitica è solitamente sconosciuta, quindi sorge un compito praticamente importante: trovare una formula empirica y=F (x; a 1, un 2,…, sono ), (1) (dove un1 , un2 ,…, unm- parametri), i cui valori a x=x,probabilmente differirebbe poco dai valori sperimentali y, (io = 1,2,…, P). Solitamente indicare la classe di funzioni (ad esempio un insieme di lineare, potenza, esponenziale, ecc.) da cui viene selezionata la funzione f(x), quindi vengono determinati i valori migliori dei parametri. Se nella formula empirica (1) sostituiamo l'iniziale X,quindi otteniamo i valori teorici YTio= f (Xio; un 1, un 2……unm) , dove io = 1,2,…, n. Differenze yioT- aio, sono chiamati deviazioni e rappresentano le distanze verticali dai punti mioal grafico della funzione empirica. Secondo il metodo dei minimi quadrati, i migliori coefficienti un1 , un2 ,…, unmsi considerano quelli per i quali la somma delle deviazioni al quadrato della funzione empirica trovata dai valori dati della funzione sarà minimo. Spieghiamo il significato geometrico del metodo dei minimi quadrati. Ogni coppia di numeri ( Xio, yio) dalla tabella di origine definisce un punto mioin superficie XOY.Usando la formula (1) per diversi valori dei coefficienti un1 , un2 ,…, unmè possibile costruire una serie di curve che sono grafici della funzione (1). Il problema è determinare i coefficienti un1 , un2 ,…, unmin modo che la somma dei quadrati delle distanze verticali dai punti mio (Xio, yio) al grafico della funzione (1) era il più piccolo (Fig. 1). La costruzione di una formula empirica consiste in due fasi: scoprire la forma generale di questa formula e determinarne i parametri migliori. Se la natura della relazione tra le quantità date x e y, allora la forma della dipendenza empirica è arbitraria. Viene data preferenza a formule semplici con buona precisione. La scelta di successo di una formula empirica dipende in gran parte dalla conoscenza del ricercatore nell'area disciplinare, utilizzando la quale può indicare la classe di funzioni da considerazioni teoriche. Di grande importanza è la rappresentazione dei dati ottenuti in sistemi di coordinate cartesiane o speciali (semilogaritmico, logaritmico, ecc.). Dalla posizione dei punti, si può approssimativamente indovinare la forma generale della dipendenza stabilendo la somiglianza tra il grafico costruito e campioni di curve note. Determinazione delle migliori quote un1 , un2,…, unminclusi nella formula empirica prodotta con metodi analitici ben noti. Per trovare un insieme di coefficienti un1 , un2 …..unm, che forniscono il minimo della funzione S definita dalla formula (2), utilizziamo la condizione necessaria per l'estremo di una funzione di più variabili - uguaglianza a zero di derivate parziali. Di conseguenza, otteniamo un sistema normale per la determinazione dei coefficienti unio(io = 1,2,…, m): Quindi, trovare i coefficienti uniosi riduce al sistema risolutivo (3). Questo sistema è semplificato se la formula empirica (1) è lineare rispetto ai parametri unio, allora il sistema (3) sarà lineare. 1.1 Relazione lineare La forma specifica del sistema (3) dipende dalla classe di formule empiriche da cui si cerca la dipendenza (1). Nel caso di una relazione lineare y=a1 +a2 Xil sistema (3) assumerà la forma: Questo sistema lineare può essere risolto con qualsiasi metodo noto (metodo di Gauss, iterazioni semplici, formule di Cramer). 1.2 Dipendenza quadratica Nel caso della dipendenza quadratica y=a1 +a2 x + a3X 2il sistema (3) assumerà la forma: 1.3 Dipendenza esponenziale In alcuni casi, come formula empirica, viene presa una funzione in cui i coefficienti incerti entrano in modo non lineare. In questo caso, a volte il problema può essere linearizzato, ad es. ridurre a lineare. Tra tali dipendenze c'è la dipendenza esponenziale y=a1 * ea2x (6) dove un 1e un 2, coefficienti indefiniti. La linearizzazione si ottiene prendendo il logaritmo di uguaglianza (6), dopo di che si ottiene la relazione ln y = ln a 1+a 2X (7) Denota ln ae ln unXrispettivamente attraverso Te C, allora la dipendenza (6) può essere scritta come t = a1 +a2 X, che ci consente di applicare le formule (4) con la sostituzione un1 sul Ce aio sul Tio 1.4 Elementi di teoria delle correlazioni Appezzamento della dipendenza funzionale restaurata y(x)in base ai risultati delle misurazioni (x io, aio),io = 1,2, K, nchiamata curva di regressione. Per verificare l'accordo della curva di regressione costruita con i risultati dell'esperimento, vengono solitamente introdotte le seguenti caratteristiche numeriche: il coefficiente di correlazione (dipendenza lineare), il rapporto di correlazione e il coefficiente di determinismo. In questo caso, i risultati sono generalmente raggruppati e presentati sotto forma di una tabella di correlazione. In ogni cella di questa tabella sono riportati i numeri niJ - quelle coppie (x, y), le cui componenti rientrano negli intervalli di raggruppamento corrispondenti per ciascuna variabile. Assumendo che le lunghezze degli intervalli di raggruppamento (per ogni variabile) siano uguali tra loro, scegli i centri x io(rispettivamente aio) di questi intervalli e il numero niJ- come base per i calcoli. Il coefficiente di correlazione è una misura della relazione lineare tra variabili aleatorie dipendenti: mostra come, in media, una delle variabili possa essere rappresentata come funzione lineare dell'altra. Il coefficiente di correlazione si calcola con la formula: dove e sono rispettivamente la media aritmetica X e a. Il coefficiente di correlazione tra variabili casuali non supera 1 in valore assoluto, tanto più |р| è vicino a 1, più stretta è la relazione lineare tra x e y. Nel caso di una correlazione non lineare, i valori medi condizionali si trovano vicino alla linea curva. In questo caso, si raccomanda di utilizzare un rapporto di correlazione come caratteristica della forza della connessione, la cui interpretazione non dipende dal tipo di dipendenza oggetto di studio. Il rapporto di correlazione si calcola con la formula: dove nio = , nF= , e il numeratore caratterizza la dispersione delle medie condizionali si, sulla media incondizionata y. È sempre. Uguaglianza = 0 corrisponde a variabili casuali non correlate; = 1 se e solo se esiste un'esatta relazione funzionale tra y e x. Nel caso di una relazione lineare y da x, il rapporto di correlazione coincide con il quadrato del coefficiente di correlazione. Valore - ? 2 viene utilizzato come indicatore della deviazione della regressione dalla linearità. Il rapporto di correlazione è una misura della correlazione y da X in qualsiasi forma, ma non può dare un'idea del grado di approssimazione dei dati empirici a una forma speciale. Per scoprire con quanta precisione la curva costruita riflette i dati empirici, viene introdotta un'altra caratteristica: il coefficiente di determinismo. Per descriverlo, considera le seguenti quantità. è la somma totale dei quadrati, dove è la media. Possiamo dimostrare la seguente uguaglianza Il primo termine è uguale a Sres = ed è chiamato somma residua dei quadrati. Caratterizza la deviazione di quelli sperimentali da quelli teorici. Il secondo termine è uguale a Sreg = 2 ed è chiamato somma di regressione dei quadrati e caratterizza la diffusione dei dati. È ovvio che la seguente uguaglianza S pieno = S ost + S reg. Il coefficiente di determinismo è determinato dalla formula: Minore è la somma residua dei quadrati rispetto alla somma totale dei quadrati, maggiore è il valore del coefficiente di determinismo R2 , che mostra quanto bene l'equazione generata dall'analisi di regressione spieghi le relazioni tra le variabili. Se è uguale a 1, allora c'è una correlazione completa con il modello, cioè non vi è alcuna differenza tra i valori y effettivi e stimati. Altrimenti, se il coefficiente di determinismo è 0, l'equazione di regressione non riesce a prevedere y valori Il coefficiente di determinismo non supera sempre il rapporto di correlazione. Nel caso in cui l'uguaglianza R 2 = allora possiamo supporre che la formula empirica costruita rifletta nel modo più accurato i dati empirici. 2. Enunciazione del problema 1. Utilizzando il metodo dei minimi quadrati, la funzione specificata nella tabella viene approssimata a) un polinomio di primo grado; b) un polinomio di secondo grado; c) dipendenza esponenziale. Per ogni dipendenza, calcola il coefficiente di determinismo. Calcolare il coefficiente di correlazione (solo nel caso a). Disegna una linea di tendenza per ogni dipendenza. Utilizzando la funzione REGR.LIN, calcolare le caratteristiche numeriche della dipendenza da. Confronta i tuoi calcoli con i risultati ottenuti utilizzando la funzione REGR.LIN. Trarre una conclusione quale delle formule ottenute approssima meglio la funzione. Scrivi un programma in uno dei linguaggi di programmazione e confronta i risultati del calcolo con quelli ottenuti sopra. 3. Dati iniziali La funzione è data in Figura 1. 4. Calcolo delle approssimazioni nel foglio di calcolo Excel Per i calcoli si consiglia di utilizzare un foglio di calcolo Microsoft Excel. E disporre i dati come mostrato nella Figura 2. Per questo inseriamo: · nelle celle A6:A30 inseriamo i valori xi . · nelle celle B6:B30 inseriamo i valori di ui . · nella cella C6 inserisci la formula =A6^ 2. · questa formula viene copiata nelle celle C7:C30. · Nella cella D6, inserisci la formula =A6*B6. · questa formula viene copiata nelle celle D7:D30. · nella cella F6, inserisci la formula =A6^4. · questa formula viene copiata nelle celle F7:F30. · nella cella G6 inseriamo la formula =A6^2*B6. · questa formula viene copiata nelle celle G7:G30. · nella cella H6, inserisci la formula =LN(B6). · questa formula viene copiata nelle celle H7:H30. · nella cella I6 inserire la formula =A6*LN(B6). · questa formula viene copiata nelle celle I7:I30. Eseguiamo i seguenti passaggi utilizzando la somma automatica · nella cella A33, inserisci la formula = SOMMA (A6: A30). · nella cella B33 inserire la formula = SOMMA (B6: B30). · nella cella C33, inserisci la formula = SOMMA (C6: C30). · nella cella D33, inserisci la formula = SOMMA (D6: D30). · nella cella E33, inserisci la formula =SOMMA (E6:E30). · nella cella F33, inserisci la formula = SOMMA (F6: F30). · nella cella G33 inserire la formula = SOMMA (G6: G30). · nella cella H33, inserisci la formula = SOMMA (H6: H30). · nella cella I33 inserire la formula = SOMMA (I6: I30). Approssimiamo la funzione y=f(x) funzione lineare y=a1 +a2X. Per determinare i coefficienti a 1e un 2usiamo il sistema (4). Utilizzando i totali della tabella 2, situata nelle celle A33, B33, C33 e D33, scriviamo il sistema (4) come risolvendo il quale, otteniamo a 1= -24,7164 e a2 = 11,63183 Pertanto, l'approssimazione lineare ha la forma y= -24,7164 + 11,63183x (12) Il sistema (11) è stato risolto utilizzando Microsoft Excel. I risultati sono presentati nella Figura 3: Nella tabella, le celle A38:B39 contengono la formula (=NBR (A35:B36)). Le celle E38:E39 contengono la formula (=MULTI(A38:B39, C35:C36)). Successivamente, approssimiamo la funzione y=f(x) funzione quadratica y=a1 +a2 x + a3 X2. Per determinare i coefficienti a 1, un 2e un 3usiamo il sistema (5). Utilizzando i totali della tabella 2, situata nelle celle A33, B33, C33, D33, E33, F33 e G33, scriviamo il sistema (5) come: Risolvendo quale, otteniamo a 1= 1,580946, a 2= -0,60819 e a3 = 0,954171 (14) Pertanto, l'approssimazione quadratica ha la forma: y \u003d 1,580946 -0,60819x + 0,954171x2 Il sistema (13) è stato risolto utilizzando Microsoft Excel. I risultati sono presentati nella Figura 4. Nella tabella, le celle A46:C48 contengono la formula (=NBR (A41:C43)). Le celle F46:F48 contengono la formula (=MULTI(A41:C43, D46:D48)). Ora approssimiamo la funzione y=f(x) funzione esponenziale y=a1 ea2x. Per determinare i coefficienti un1 e un2 prendi il logaritmo dei valori yioe utilizzando i totali della tabella 2, situata nelle celle A26, C26, H26 e I26, otteniamo il sistema: dove ñ = ln(a1 ). Risolvendo il sistema (10) troviamo c =0,506435, a2 = 0.409819. Dopo il potenziamento, otteniamo a1 = 1,659365. Pertanto, l'approssimazione esponenziale ha la forma y = 1,659365*e0,4098194x Il sistema (15) è stato risolto utilizzando Microsoft Excel. I risultati sono mostrati nella Figura 5. Nella tabella, le celle A55:B56 contengono la formula (=NBR (A51:B52)). Le celle E54:E56 contengono la formula (=MULTIPLE(A51:B52, C51:C52)). La cella E56 contiene la formula =EXP(E54). Calcola la media aritmetica di xey usando le formule: Risultati del calcolo x e yGli strumenti di Microsoft Excel sono illustrati nella Figura 6. La cella B58 contiene la formula =A33/25. La cella B59 contiene la formula =B33/25. Tavolo 2 Spieghiamo come viene compilata la tabella nella Figura 7. Le celle A6:A33 e B6:B33 sono già riempite (vedi Figura 2). · nella cella J6, inserisci la formula =(A6-$B$58)*(B6-$B$59). · questa formula viene copiata nelle celle J7:J30. · nella cella K6, inserisci la formula =(A6-$B$58)^ 2. · questa formula viene copiata nelle celle K7:K30. · nella cella L6, inserisci la formula =(B1-$B$59)^2. · questa formula viene copiata nelle celle L7:L30. · nella cella M6 inserisci la formula =($E$38+$E$39*A6-B6)^2. · questa formula viene copiata nelle celle M7:M30. · nella cella N6, inserisci la formula =($F$46 +$F$47*A6 +$F$48*A6 L6-B6)^2. · questa formula viene copiata nelle celle N7:N30. · nella cella O6, inserisci la formula =($E$56*EXP ($E$55*A6) - B6)^2. · questa formula viene copiata nelle celle O7:O30. I passaggi successivi vengono eseguiti utilizzando la somma automatica. · nella cella J33, inserisci la formula =CYMM (J6:J30). · nella cella K33, inserisci la formula = SOMMA (K6: K30). · nella cella L33, inserisci la formula =CYMM (L6:L30). · nella cella M33 inserire la formula = SOMMA (M6: M30). · nella cella N33 inserire la formula = SOMMA (N6: N30). · nella cella O33, inserisci la formula = SOMMA (06:030). Ora calcoliamo il coefficiente di correlazione usando la formula (8) (solo per approssimazione lineare) e il coefficiente di determinismo usando la formula (10). I risultati dei calcoli con Microsoft Excel sono mostrati nella Figura 7. Nella tabella 8, la cella B61 contiene la formula =J33/(K33*L33^(1/2). La cella B62 contiene la formula =1 - M33/L33. La cella B63 contiene la formula =1 - N33/L33. La cella B64 contiene formula =1 - O33/L33. Un'analisi dei risultati del calcolo mostra che l'approssimazione quadratica descrive al meglio i dati sperimentali. 4.1 Rappresentazione grafica in Excel Selezioniamo le celle A1:A25, dopodiché passeremo alla procedura guidata del grafico. Scegliamo un grafico a dispersione. Dopo aver costruito il grafico, fare clic con il pulsante destro del mouse sulla linea del grafico e scegliere di aggiungere una linea di tendenza (rispettivamente lineare, esponenziale, potenza e polinomio di secondo grado). Grafico di approssimazione lineare Grafico di approssimazione quadratica Grafico di adattamento esponenziale. 5. Approssimazione di una funzione utilizzando MathCAD L'approssimazione dei dati tenendo conto dei loro parametri statistici si riferisce a problemi di regressione. Solitamente si verificano durante l'elaborazione di dati sperimentali ottenuti a seguito di misurazioni di processi o fenomeni fisici di natura statistica (come misurazioni in radiometria e geofisica nucleare) o ad alto livello di interferenza (rumore). Il compito dell'analisi di regressione è la selezione delle formule matematiche che meglio descrivono i dati sperimentali. .1 Regressione lineare La regressione lineare nel sistema Mathcad viene eseguita sui vettori dell'argomento Xe letture Y funzioni: intercettare (x, y)- calcola il parametro ma1 , spostamento verticale della retta di regressione (vedi fig.) pendenza (x, y)- calcola il parametro un2 , pendenza della retta di regressione (vedi figura) y(x) = a1+a2*x Funzione corr(y, y(x))calcola Coefficiente di correlazione di Pearson.Più è vicino a lui 1, quanto più accuratamente i dati in elaborazione corrispondono ad una relazione lineare (vedi Fig.) .2 Regressione polinomiale La regressione polinomiale unidimensionale con un grado n arbitrario del polinomio e con coordinate campionarie arbitrarie in Mathcad viene eseguita dalle funzioni: regresso(x, y, n)- calcola un vettore S,che contiene i coefficienti aipolinomio n esimo grado; Valori di coefficiente aipuò essere estratto dal vettore Sfunzione sottomatrice (S, 3, lunghezza(S) - 1, 0, 0). I valori ottenuti dei coefficienti vengono utilizzati nell'equazione di regressione y(x) = a1+a2*x+a3*x2 (vedi foto) .3 Regressione non lineare Per semplici formule di approssimazione tipiche, vengono fornite alcune funzioni di regressione non lineare, in cui i parametri della funzione sono selezionati dal programma Mathcad. Tra questi c'è la funzione exfit(x, y, s),che restituisce un vettore contenente i coefficienti a1, a2e a3funzione esponenziale y(x) = a1 ^exp (a2x) + a3.V vettore Svengono inseriti i valori iniziali dei coefficienti a1, a2e a3prima approssimazione. Conclusione L'analisi dei risultati del calcolo mostra che l'approssimazione lineare descrive al meglio i dati sperimentali. I risultati ottenuti utilizzando il programma MathCAD corrispondono completamente ai valori ottenuti utilizzando Excel. Questo indica la correttezza dei calcoli. Bibliografia
TutoraggioHai bisogno di aiuto per imparare un argomento?
I nostri esperti ti consiglieranno o forniranno servizi di tutoraggio su argomenti di tuo interesse. L'approssimazione dei dati sperimentali è un metodo basato sulla sostituzione dei dati ottenuti sperimentalmente con una funzione analitica che più da vicino passa o coincide nei punti nodali con i valori iniziali (dati ottenuti durante l'esperimento o l'esperimento). Esistono attualmente due modi per definire una funzione analitica: Costruendo un polinomio di interpolazione di n gradi che passa direttamente attraverso tutti i punti data matrice di dati. In questo caso, la funzione di approssimazione è rappresentata come: un polinomio di interpolazione nella forma di Lagrange o un polinomio di interpolazione nella forma di Newton. Costruendo un polinomio approssimativo di n gradi che passa vicino ai punti dall'array di dati specificato. Pertanto, la funzione di approssimazione smussa tutti i rumori casuali (o errori) che possono verificarsi durante l'esperimento: i valori misurati durante l'esperimento dipendono da fattori casuali che fluttuano secondo le proprie leggi casuali (misurazioni o errori strumentali, imprecisioni o sperimentali errori). In questo caso, la funzione di approssimazione è determinata dal metodo dei minimi quadrati. Metodo dei minimi quadrati(nella letteratura inglese Ordinary Least Squares, OLS) è un metodo matematico basato sulla definizione di una funzione di approssimazione, che è costruita nella più stretta vicinanza ai punti da una data matrice di dati sperimentali. La prossimità tra la funzione iniziale e quella di approssimazione F(x) è determinata da una misura numerica, ovvero: la somma delle deviazioni al quadrato dei dati sperimentali dalla curva di approssimazione F(x) deve essere la più piccola. Curva di adattamento costruita con il metodo dei minimi quadrati Viene utilizzato il metodo dei minimi quadrati: Risolvere sistemi di equazioni sovradeterminati quando il numero di equazioni supera il numero di incognite; Cercare una soluzione nel caso di sistemi di equazioni non lineari ordinari (non sovradeterminati); Per approssimare i valori dei punti mediante una funzione di approssimazione. La funzione di approssimazione con il metodo dei minimi quadrati è determinata dalla condizione della somma minima delle deviazioni quadrate della funzione di approssimazione calcolata da una data matrice di dati sperimentali. Questo criterio del metodo dei minimi quadrati è scritto come la seguente espressione:
Valori della funzione di approssimazione calcolata in punti nodali, Matrice specificata di dati sperimentali in punti nodali. Un criterio quadratico ha una serie di proprietà "buone", come la differenziabilità, fornendo una soluzione unica al problema di approssimazione con funzioni di approssimazione polinomiale. A seconda delle condizioni del problema, la funzione di approssimazione è un polinomio di grado m Il grado della funzione di approssimazione non dipende dal numero di punti nodali, ma la sua dimensione deve essere sempre inferiore alla dimensione (numero di punti) della matrice data di dati sperimentali.
∙ Se il grado della funzione di approssimazione è m=1, allora approssimiamo la funzione tabella con una retta (regressione lineare). ∙ Se il grado della funzione di approssimazione è m=2, allora approssimiamo la funzione tabellare con una parabola quadratica (approssimazione quadratica). ∙ Se il grado della funzione di approssimazione è m=3, allora approssimiamo la funzione tabellare con una parabola cubica (approssimazione cubica). Nel caso generale, quando si vuole costruire un polinomio approssimativo di grado m per dati valori tabulari, la condizione per la somma minima delle deviazioni al quadrato su tutti i punti nodali si riscrive nella forma seguente:
Il numero di valori di tabella specificati. Condizione necessaria per l'esistenza di un minimo di una funzione è l'uguaglianza a zero delle sue derivate parziali rispetto a variabili incognite
Trasformiamo il sistema lineare di equazioni risultante: apriamo le parentesi e spostiamo i termini liberi sul lato destro dell'espressione. Di conseguenza, il sistema risultante di espressioni algebriche lineari sarà scritto nella forma seguente:
Questo sistema di espressioni algebriche lineari può essere riscritto in forma matriciale:
Di conseguenza, è stato ottenuto un sistema di equazioni lineari di dimensione m + 1, che consiste in m + 1 incognite. Questo sistema può essere risolto utilizzando qualsiasi metodo per la risoluzione di equazioni algebriche lineari (ad esempio il metodo di Gauss). Come risultato della soluzione, si troveranno parametri sconosciuti della funzione di approssimazione che forniscono la somma minima delle deviazioni al quadrato della funzione di approssimazione dai dati originali, cioè la migliore approssimazione quadratica possibile. Va ricordato che se cambia anche un solo valore dei dati iniziali, tutti i coefficienti cambieranno i loro valori, poiché sono completamente determinati dai dati iniziali. Approssimazione dei dati iniziali per dipendenza lineare (regressione lineare) Ad esempio, si consideri il metodo per determinare la funzione di approssimazione, data come relazione lineare. Secondo il metodo dei minimi quadrati, la condizione per la somma minima delle deviazioni al quadrato è scritta come segue: Coordinate dei punti nodali della tavola; Coefficienti sconosciuti della funzione di approssimazione, che è data come relazione lineare. Condizione necessaria per l'esistenza di un minimo di una funzione è l'uguaglianza a zero delle sue derivate parziali rispetto a variabili incognite. Di conseguenza, otteniamo il seguente sistema di equazioni:
Trasformiamo il sistema lineare di equazioni risultante.
Risolviamo il risultante sistema di equazioni lineari. I coefficienti della funzione di approssimazione nella forma analitica sono determinati come segue (metodo di Cramer):
Questi coefficienti forniscono la costruzione di una funzione di approssimazione lineare secondo il criterio per ridurre al minimo la somma dei quadrati della funzione di approssimazione da determinati valori tabulari (dati sperimentali). Algoritmo per implementare il metodo dei minimi quadrati 1. Dati iniziali: Data una matrice di dati sperimentali con il numero di misurazioni N Viene fornito il grado del polinomio approssimativo (m). 2. Algoritmo di calcolo: 2.1. I coefficienti sono determinati per costruire un sistema di equazioni con dimensione
Coefficienti del sistema di equazioni (lato sinistro dell'equazione)
Membri liberi del sistema di equazioni lineari (lato destro dell'equazione)
2.2. Formazione di un sistema di equazioni lineari con dimensione.
2.3. Soluzione di un sistema di equazioni lineari per determinare i coefficienti incogniti del polinomio approssimativo di grado m. 2.4 Determinazione della somma delle deviazioni al quadrato del polinomio approssimativo dai valori iniziali su tutti i punti nodali
Il valore trovato della somma delle deviazioni al quadrato è il minimo possibile. Approssimazione con altre funzioni Va notato che quando si approssimano i dati iniziali secondo il metodo dei minimi quadrati, una funzione logaritmica, una funzione esponenziale e una funzione di potenza vengono talvolta utilizzate come funzione di approssimazione. Approssimazione logaritmica Si consideri il caso in cui la funzione di approssimazione è data da una funzione logaritmica della forma: | ||