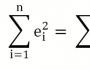Aproximarea datelor experimentale. Metoda celor mai mici pătrate. Aproximarea unei funcții prin metoda celor mai mici pătrate Folosind metoda celor mai mici pătrate pentru a aproxima
După aliniere, obținem o funcție de următoarea formă: g (x) = x + 1 3 + 1 .
Putem aproxima aceste date cu o relație liniară y = a x + b calculând parametrii corespunzători. Pentru a face acest lucru, va trebui să aplicăm așa-numita metodă a celor mai mici pătrate. De asemenea, va trebui să faceți un desen pentru a verifica care linie va alinia cel mai bine datele experimentale.
Ce este exact MOL (metoda celor mai mici pătrate)
Principalul lucru pe care trebuie să-l facem este să găsim astfel de coeficienți de dependență liniară la care valoarea funcției a două variabile F (a, b) = ∑ i = 1 n (yi - (axi + b)) 2 va fi cea mai mică . Cu alte cuvinte, pentru anumite valori ale lui a și b, suma abaterilor pătrate ale datelor prezentate de la linia dreaptă rezultată va avea o valoare minimă. Acesta este sensul metodei celor mai mici pătrate. Tot ce trebuie să facem pentru a rezolva exemplul este să găsim extremul funcției a două variabile.
Cum se obțin formule pentru calcularea coeficienților
Pentru a deriva formule de calcul a coeficientilor este necesara alcatuirea si rezolvarea unui sistem de ecuatii cu doua variabile. Pentru a face acest lucru, calculăm derivatele parțiale ale expresiei F (a , b) = ∑ i = 1 n (y i - (a x i + b)) 2 față de a și b și le echivalăm cu 0 .
δ F (a , b) δ a = 0 δ F (a , b) δ b = 0 ⇔ - 2 ∑ i = 1 n (yi - (axi + b)) xi = 0 - 2 ∑ i = 1 n ( yi - (axi + b)) = 0 ⇔ a ∑ i = 1 nxi 2 + b ∑ i = 1 nxi = ∑ i = 1 nxiyia ∑ i = 1 nxi + ∑ i = 1 nb = ∑ i = 1 nyi ⇔ a ∑ i = 1 nxi 2 + b ∑ i = 1 nxi = ∑ i = 1 nxiyia ∑ i = 1 nxi + nb = ∑ i = 1 nyi
Pentru a rezolva un sistem de ecuații, puteți folosi orice metodă, cum ar fi substituția sau metoda lui Cramer. Ca rezultat, ar trebui să obținem formule care calculează coeficienții folosind metoda celor mai mici pătrate.
n ∑ i = 1 n x i y i - ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n - ∑ i = 1 n x i 2 b = ∑ i = 1 n y i - a ∑ i = 1 n x i n
Am calculat valorile variabilelor pentru care funcția
F (a , b) = ∑ i = 1 n (y i - (a x i + b)) 2 va lua valoarea minimă. În al treilea paragraf, vom demonstra de ce este așa.
Aceasta este aplicarea metodei celor mai mici pătrate în practică. Formula sa, care este folosită pentru a găsi parametrul a , include ∑ i = 1 n x i , ∑ i = 1 n y i , ∑ i = 1 n x i y i , ∑ i = 1 n x i 2 , iar parametrul
n - denotă cantitatea de date experimentale. Vă sfătuim să calculați fiecare sumă separat. Valoarea coeficientului b se calculează imediat după a .
Să revenim la exemplul inițial.
Exemplul 1
Aici avem n egal cu cinci. Pentru a face mai convenabil calculul sumelor necesare incluse în formulele coeficientului, completăm tabelul.
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | ∑ i = 1 5 | |
| x i | 0 | 1 | 2 | 4 | 5 | 12 |
| y eu | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 | 12 , 9 |
| x i y i | 0 | 2 , 4 | 5 , 2 | 11 , 2 | 15 | 33 , 8 |
| x i 2 | 0 | 1 | 4 | 16 | 25 | 46 |
Soluţie
Al patrulea rând conține datele obținute prin înmulțirea valorilor din al doilea rând cu valorile celui de-al treilea pentru fiecare individ i. A cincea linie conține datele din al doilea pătrat. Ultima coloană arată sumele valorilor rândurilor individuale.
Să folosim metoda celor mai mici pătrate pentru a calcula coeficienții a și b de care avem nevoie. Pentru a face acest lucru, înlocuiți valorile dorite din ultima coloană și calculați sumele:
n ∑ i = 1 nxiyi - ∑ i = 1 nxi ∑ i = 1 nyin ∑ i = 1 n - ∑ i = 1 nxi 2 b = ∑ i = 1 nyi - a ∑ i = 1 nxin ⇒ a = 5 33, 8 - 12 12, 9 5 46 - 12 2 b = 12, 9 - a 12 5 ⇒ a ≈ 0, 165 b ≈ 2, 184
Am obținut că linia dreaptă de aproximare dorită va arăta ca y = 0, 165 x + 2, 184. Acum trebuie să determinăm care linie va aproxima cel mai bine datele - g (x) = x + 1 3 + 1 sau 0 , 165 x + 2 , 184 . Să facem o estimare folosind metoda celor mai mici pătrate.
Pentru a calcula eroarea, trebuie să găsim sumele abaterilor pătrate ale datelor din liniile σ 1 = ∑ i = 1 n (yi - (axi + bi)) 2 și σ 2 = ∑ i = 1 n (yi - g (xi)) 2 , valoarea minimă va corespunde unei linii mai potrivite.
σ 1 = ∑ i = 1 n (yi - (axi + bi)) 2 = = ∑ i = 1 5 (yi - (0 , 165 xi + 2 , 184)) 2 ≈ 0 , 019 σ 2 = ∑ i = 1 n (yi - g (xi)) 2 = = ∑ i = 1 5 (yi - (xi + 1 3 + 1)) 2 ≈ 0 , 096
Răspuns: deoarece σ 1< σ 2 , то прямой, наилучшим образом аппроксимирующей исходные данные, будет
y = 0 , 165 x + 2 , 184 .
Metoda celor mai mici pătrate este prezentată clar în ilustrația grafică. Linia roșie marchează linia dreaptă g (x) = x + 1 3 + 1, linia albastră marchează y = 0, 165 x + 2, 184. Datele brute sunt marcate cu puncte roz.
Să explicăm de ce sunt necesare exact aproximări de acest tip.
Ele pot fi utilizate în probleme care necesită netezirea datelor, precum și în acelea în care datele trebuie interpolate sau extrapolate. De exemplu, în problema discutată mai sus, s-ar putea găsi valoarea mărimii observate y la x = 3 sau la x = 6 . Am dedicat un articol separat unor astfel de exemple.
Dovada metodei LSM
Pentru ca funcția să ia valoarea minimă pentru a și b calculat, este necesar ca la un punct dat matricea formei pătratice a diferențială a funcției de forma F (a, b) = ∑ i = 1 n ( yi - (axi + b)) 2 fie definit pozitiv. Să vă arătăm cum ar trebui să arate.
Exemplul 2
Avem o diferenţială de ordinul doi de următoarea formă:
d 2 F (a ; b) = δ 2 F (a ; b) δ a 2 d 2 a + 2 δ 2 F (a ; b) δ a δ bdadb + δ 2 F (a ; b) δ b 2 d 2b
Soluţie
δ 2 F (a ; b) δ a 2 = δ δ F (a ; b) δ a δ a = = δ - 2 ∑ i = 1 n (yi - (axi + b)) xi δ a = 2 ∑ i = 1 n (xi) 2 δ 2 F (a ; b) δ a δ b = δ δ F (a ; b) δ a δ b = = δ - 2 ∑ i = 1 n (yi - (axi + b) ) xi δ b = 2 ∑ i = 1 nxi δ 2 F (a ; b) δ b 2 = δ δ F (a ; b) δ b δ b = δ - 2 ∑ i = 1 n (yi - (axi + b)) δ b = 2 ∑ i = 1 n (1) = 2 n
Cu alte cuvinte, se poate scrie astfel: d 2 F (a ; b) = 2 ∑ i = 1 n (x i) 2 d 2 a + 2 2 ∑ x i i = 1 n d a d b + (2 n) d 2 b .
Am obținut o matrice de formă pătratică M = 2 ∑ i = 1 n (x i) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n .
În acest caz, valorile elementelor individuale nu se vor schimba în funcție de a și b. Este această matrice pozitivă definită? Pentru a răspunde la această întrebare, să verificăm dacă minorele sale unghiulare sunt pozitive.
Calculați primul unghiular de ordinul întâi: 2 ∑ i = 1 n (x i) 2 > 0 . Deoarece punctele x i nu coincid, inegalitatea este strictă. Vom ține cont de acest lucru în calculele ulterioare.
Calculăm minorul unghiular de ordinul doi:
d e t (M) = 2 ∑ i = 1 n (x i) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n = 4 n ∑ i = 1 n (x i) 2 - ∑ i = 1 n x i 2
După aceea, trecem la demonstrarea inegalității n ∑ i = 1 n (x i) 2 - ∑ i = 1 n x i 2 > 0 folosind inducția matematică.
- Să verificăm dacă această inegalitate este valabilă pentru n arbitrar. Să luăm 2 și să calculăm:
2 ∑ i = 1 2 (xi) 2 - ∑ i = 1 2 xi 2 = 2 x 1 2 + x 2 2 - x 1 + x 2 2 = = x 1 2 - 2 x 1 x 2 + x 2 2 = x 1 + x 2 2 > 0
Am obținut egalitatea corectă (dacă valorile x 1 și x 2 nu se potrivesc).
- Să presupunem că această inegalitate va fi adevărată pentru n , i.e. n ∑ i = 1 n (x i) 2 - ∑ i = 1 n x i 2 > 0 – adevărat.
- Acum să demonstrăm validitatea pentru n + 1 , adică. că (n + 1) ∑ i = 1 n + 1 (xi) 2 - ∑ i = 1 n + 1 xi 2 > 0 dacă n ∑ i = 1 n (xi) 2 - ∑ i = 1 nxi 2 > 0 .
Noi calculăm:
(n + 1) ∑ i = 1 n + 1 (xi) 2 - ∑ i = 1 n + 1 xi 2 = = (n + 1) ∑ i = 1 n (xi) 2 + xn + 1 2 - ∑ i = 1 nxi + xn + 1 2 = = n ∑ i = 1 n (xi) 2 + n xn + 1 2 + ∑ i = 1 n (xi) 2 + xn + 1 2 - - ∑ i = 1 nxi 2 + 2 xn + 1 ∑ i = 1 nxi + xn + 1 2 = = ∑ i = 1 n (xi) 2 - ∑ i = 1 nxi 2 + n xn + 1 2 - xn + 1 ∑ i = 1 nxi + ∑ i = 1 n (xi) 2 = = ∑ i = 1 n (xi) 2 - ∑ i = 1 nxi 2 + xn + 1 2 - 2 xn + 1 x 1 + x 1 2 + + xn + 1 2 - 2 xn + 1 x 2 + x 2 2 + . . . + xn + 1 2 - 2 xn + 1 x 1 + xn 2 = = n ∑ i = 1 n (xi) 2 - ∑ i = 1 nxi 2 + + (xn + 1 - x 1) 2 + (xn + 1) - x 2) 2 + . . . + (x n - 1 - x n) 2 > 0
Expresia cuprinsă între acolade va fi mai mare decât 0 (pe baza a ceea ce am presupus la pasul 2), iar restul termenilor va fi mai mare decât 0 deoarece toți sunt pătrate de numere. Am dovedit inegalitatea.
Răspuns: a și b găsite vor corespunde celei mai mici valori a funcției F (a, b) = ∑ i = 1 n (yi - (axi + b)) 2, ceea ce înseamnă că sunt parametrii doriti ai metodei celor mai mici pătrate (LSM).
Dacă observați o greșeală în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter
Are multe aplicații, deoarece permite o reprezentare aproximativă a unei anumite funcții de către altele mai simple. LSM poate fi extrem de util în procesarea observațiilor și este utilizat în mod activ pentru a estima unele cantități din rezultatele măsurătorilor altora care conțin erori aleatoare. În acest articol, veți învăța cum să implementați calculele celor mai mici pătrate în Excel.
Enunțarea problemei pe un exemplu specific
Să presupunem că există doi indicatori X și Y. Mai mult, Y depinde de X. Deoarece OLS este de interes pentru noi din punct de vedere al analizei de regresie (în Excel, metodele sale sunt implementate folosind funcții încorporate), ar trebui să procedăm imediat a lua în considerare o problemă specifică.
Deci, să fie X aria de vânzare a unui magazin alimentar, măsurată în metri pătrați, iar Y să fie cifra de afaceri anuală, definită în milioane de ruble.
Se cere sa se faca o previziune a ce cifra de afaceri (Y) va avea magazinul daca are unul sau altul spatiu comercial. Evident, funcția Y = f (X) este în creștere, deoarece hipermarketul vinde mai multe mărfuri decât taraba.
Câteva cuvinte despre corectitudinea datelor inițiale utilizate pentru predicție
Să presupunem că avem un tabel construit cu date pentru n magazine.
Conform statisticilor matematice, rezultatele vor fi mai mult sau mai puțin corecte dacă se examinează datele de pe cel puțin 5-6 obiecte. De asemenea, rezultatele „anomale” nu pot fi folosite. În special, un mic butic de elită poate avea o cifră de afaceri de multe ori mai mare decât cifra de afaceri a magazinelor mari din clasa „masmarket”.
Esența metodei
Datele din tabel pot fi afișate pe planul cartezian ca puncte M 1 (x 1, y 1), ... M n (x n, y n). Acum soluția problemei se va reduce la selectarea unei funcții de aproximare y = f (x), care are un grafic care trece cât mai aproape de punctele M 1, M 2, .. M n .
Desigur, puteți utiliza un polinom de grad înalt, dar această opțiune nu este doar dificil de implementat, ci pur și simplu incorectă, deoarece nu va reflecta tendința principală care trebuie detectată. Soluția cea mai rezonabilă este să căutați o dreaptă y = ax + b, care aproximează cel mai bine datele experimentale și, mai precis, coeficienții - a și b.
Scorul de precizie
Pentru orice aproximare, evaluarea acurateței sale este de o importanță deosebită. Notați cu e i diferența (abaterea) dintre valorile funcționale și experimentale pentru punctul x i , adică e i = y i - f (x i).
Evident, pentru a evalua acuratețea aproximării, puteți utiliza suma abaterilor, adică, atunci când alegeți o linie dreaptă pentru o reprezentare aproximativă a dependenței lui X de Y, ar trebui să se acorde preferință celei care are cea mai mică valoare a suma ei în toate punctele luate în considerare. Cu toate acestea, nu totul este atât de simplu, deoarece împreună cu abaterile pozitive, practic vor fi și negative.
Puteți rezolva problema folosind modulele de abatere sau pătratele acestora. Această din urmă metodă este cea mai utilizată. Este folosit în multe domenii, inclusiv în analiza regresiei (în Excel, implementarea sa se realizează folosind două funcții încorporate) și s-a dovedit de mult timp a fi eficient.
Metoda celor mai mici pătrate
În Excel, după cum știți, există o funcție de asumare automată încorporată care vă permite să calculați valorile tuturor valorilor situate în intervalul selectat. Astfel, nimic nu ne va împiedica să calculăm valoarea expresiei (e 1 2 + e 2 2 + e 3 2 + ... e n 2).
În notație matematică, aceasta arată astfel:

Deoarece inițial a fost luată decizia de a aproxima folosind o linie dreaptă, avem:

Astfel, sarcina de a găsi o linie dreaptă care descrie cel mai bine o relație specifică între X și Y echivalează cu calcularea minimului unei funcții a două variabile:

Acest lucru necesită egalarea la zero derivate parțiale în raport cu noile variabile a și b și rezolvarea unui sistem primitiv format din două ecuații cu 2 necunoscute de forma:

După transformări simple, inclusiv împărțirea la 2 și manipularea sumelor, obținem:

Rezolvând-o, de exemplu, prin metoda lui Cramer, obținem un punct staționar cu anumiți coeficienți a * și b * . Acesta este minimul, adică pentru a prezice ce cifră de afaceri va avea magazinul pentru o anumită zonă, este potrivită linia dreaptă y = a * x + b *, care este un model de regresie pentru exemplul în cauză. Desigur, nu vă va permite să găsiți rezultatul exact, dar vă va ajuta să vă faceți o idee dacă cumpărarea unui magazin cu credit pentru o anumită zonă va fi rentabilă.
Cum se implementează metoda celor mai mici pătrate în Excel
Excel are o funcție pentru calcularea valorii celor mai mici pătrate. Are următoarea formă: TREND (valori Y cunoscute; valori X cunoscute; valori X noi; constantă). Să aplicăm formula pentru calcularea MOL în Excel în tabelul nostru.
Pentru a face acest lucru, în celula în care ar trebui să fie afișat rezultatul calculului folosind metoda celor mai mici pătrate în Excel, introduceți semnul „=” și selectați funcția „TENDINȚA”. În fereastra care se deschide, completați câmpurile corespunzătoare, evidențiind:
- interval de valori cunoscute pentru Y (în acest caz date pentru cifra de afaceri);
- interval x 1 , …x n , adică dimensiunea spațiului comercial cu amănuntul;
- și valorile cunoscute și necunoscute ale lui x, pentru care trebuie să aflați dimensiunea cifrei de afaceri (pentru informații despre locația lor pe foaia de lucru, consultați mai jos).
În plus, există o variabilă logică „Const” în formulă. Dacă introduceți 1 în câmpul corespunzător, atunci aceasta va însemna că trebuie efectuate calcule, presupunând că b \u003d 0.
Dacă trebuie să cunoașteți prognoza pentru mai mult de o valoare x, atunci după introducerea formulei, nu trebuie să apăsați „Enter”, ci trebuie să introduceți combinația „Shift” + „Control” + „Enter” („Enter” ) pe tastatură.
Unele caracteristici
Analiza de regresie poate fi accesibilă chiar și pentru manechin. Formula Excel pentru prezicerea valorii unui tablou de variabile necunoscute – „TENDINȚA” – poate fi folosită chiar și de cei care nu au auzit niciodată de metoda celor mai mici pătrate. Este suficient doar să cunoști câteva caracteristici ale muncii sale. În special:
- Dacă plasați intervalul de valori cunoscute ale variabilei y într-un rând sau coloană, atunci fiecare rând (coloană) cu valori cunoscute ale lui x va fi perceput de program ca o variabilă separată.
- Dacă intervalul cu x cunoscut nu este specificat în fereastra TREND, atunci în cazul utilizării funcției în Excel, programul o va considera ca o matrice formată din numere întregi, al căror număr corespunde intervalului cu valorile date. a variabilei y.
- Pentru a scoate o matrice de valori „prevăzute”, expresia tendinței trebuie introdusă ca formulă matrice.
- Dacă nu sunt specificate noi valori x, atunci funcția TREND le consideră egale cu cele cunoscute. Dacă nu sunt specificate, atunci tabloul 1 este luat ca argument; 2; 3; 4;…, care este proporțional cu intervalul cu parametrii deja dați y.
- Intervalul care conține noile valori x trebuie să aibă aceleași sau mai multe rânduri sau coloane ca și intervalul cu valorile y date. Cu alte cuvinte, trebuie să fie proporțional cu variabilele independente.
- O matrice cu valori x cunoscute poate conține mai multe variabile. Cu toate acestea, dacă vorbim doar despre unul, atunci este necesar ca intervalele cu valorile date ale lui x și y să fie proporționale. În cazul mai multor variabile, este necesar ca intervalul cu valorile y date să se încadreze într-o coloană sau un rând.

Funcția FORECAST
Este implementat folosind mai multe funcții. Una dintre ele se numește „PREDICȚIE”. Este similar cu TREND, adică oferă rezultatul calculelor folosind metoda celor mai mici pătrate. Cu toate acestea, numai pentru un X, pentru care valoarea lui Y este necunoscută.
Acum cunoașteți formulele Excel pentru manechine care vă permit să preziceți valoarea viitoarei valori a unui indicator în funcție de o tendință liniară.
3. Aproximarea funcțiilor folosind metoda
cele mai mici pătrate
Metoda celor mai mici pătrate este utilizată la procesarea rezultatelor experimentului pentru aproximări (aproximații) date experimentale formula analitica. Forma specifică a formulei este aleasă, de regulă, din considerente fizice. Aceste formule pot fi:
![]()
![]()
si altii.
Esența metodei celor mai mici pătrate este următoarea. Lăsați rezultatele măsurătorii să fie prezentate în tabel:
|
masa 4 |
||||
|
x n |
||||
|
y n |
||||
|
(3.1) |
unde f este o funcție cunoscută, a 0 , a 1 , …, a m - parametri constanți necunoscuți, ale căror valori trebuie găsite. În metoda celor mai mici pătrate, aproximarea funcției (3.1) la dependența experimentală este considerată a fi cea mai bună dacă condiția
|
(3.2) |
adică sume A abaterile pătrate ale funcției analitice dorite de la dependența experimentală ar trebui să fie minime .
Rețineți că funcția Q numit inviscid.

De la discrepanța

atunci are un minim. O condiție necesară pentru minimumul unei funcții a mai multor variabile este egalitatea la zero a tuturor derivatelor parțiale ale acestei funcții în raport cu parametrii. Astfel, găsirea celor mai bune valori ale parametrilor funcției de aproximare (3.1), adică acele valori pentru care Q = Q (a 0 , a 1 , …, a m ) este minimă, se reduce la rezolvarea sistemului de ecuații:
|
(3.3) |
Metodei celor mai mici pătrate i se poate da următoarea interpretare geometrică: dintr-o familie infinită de drepte de un tip dat se găsește o dreaptă pentru care suma diferențelor pătrate în ordonatele punctelor experimentale și ordonatele corespunzătoare ale punctelor. găsit prin ecuația acestei drepte va fi cel mai mic.
Găsirea parametrilor unei funcții liniare
Fie ca datele experimentale să fie reprezentate printr-o funcție liniară:
Este necesar să alegeți astfel de valori a și b , pentru care funcția
|
(3.4) |
va fi minim. Condițiile necesare pentru minimul funcției (3.4) se reduc la sistemul de ecuații:
|
|
După transformări, obținem un sistem de două ecuații liniare cu două necunoscute:
|
|
(3.5) |
rezolvând care, găsim valorile dorite ale parametrilor a și b .
Găsirea parametrilor unei funcții pătratice
Dacă funcția de aproximare este o dependență pătratică
apoi parametrii săi a, b, c găsiți din condiția minimă a funcției:
|
(3.6) |
Condițiile minime pentru funcția (3.6) se reduc la sistemul de ecuații:
|
|
După transformări, obținem un sistem de trei ecuații liniare cu trei necunoscute:
|
|
(3.7) |
la rezolvând care găsim valorile dorite ale parametrilor a, b și c.
Exemplu . Să se obțină următorul tabel de valori ca rezultat al experimentului x și y:
|
masa 5 |
||||||||
|
y eu |
0,705 |
0,495 |
0,426 |
0,357 |
0,368 |
0,406 |
0,549 |
0,768 |
Este necesară aproximarea datelor experimentale prin funcții liniare și pătratice.
Soluţie. Găsirea parametrilor funcțiilor de aproximare se reduce la rezolvarea sistemelor de ecuații liniare (3.5) și (3.7). Pentru a rezolva problema, folosim un procesor de foi de calcul excela.
1. Mai întâi legăm foile 1 și 2. Introduceți valorile experimentale x i și y euîn coloane A și B, începând de la a doua linie (în primul rând punem titlurile coloanelor). Apoi calculăm sumele pentru aceste coloane și le punem în al zecelea rând.
În coloanele C–G plasează calculul și respectiv însumarea
2. Desprindeți foile. Calculele ulterioare se vor efectua în mod similar pentru dependența liniară de Foaia 1 și pentru dependența pătratică de Foaia 2.
3. Sub tabelul rezultat, formăm o matrice de coeficienți și un vector coloană de termeni liberi. Să rezolvăm sistemul de ecuații liniare conform următorului algoritm:
Pentru a calcula matricea inversă și a înmulți matrice, folosim Maestru funcții si functii MOBRȘi MUMNOZH.
4. În blocul de celule H2: H 9 pe baza coeficienților obținuți, calculăm valorile aproximării polinomy eu calc., în blocul I 2: I 9 - abateri D y i = y eu exp. - y eu calc., în coloana J - discrepanța:
Tabelele obținute și construite folosind Chart Wizards graficele sunt prezentate în figurile 6, 7, 8.

Orez. 6. Tabel pentru calcularea coeficienților unei funcții liniare,
aproximând date experimentale.

Orez. 7. Tabel pentru calcularea coeficienților unei funcții pătratice,
aproximânddate experimentale.

Orez. 8. Reprezentarea grafică a rezultatelor aproximării
date experimentale funcții liniare și pătratice.
Răspuns. Datele experimentale au fost aproximate prin dependența liniară y = 0,07881 X + 0,442262 cu rezidual Q = 0,165167 și dependență pătratică y = 3,115476 X 2 – 5,2175 X + 2,529631 cu rezidual Q = 0,002103 .
Sarcini. Aproximați funcția dată de funcții tabulare, liniare și pătratice.
|
Tabelul 6 |
|||||||||
|
№0 |
X |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
|
y |
3,030 |
3,142 |
3,358 |
3,463 |
3,772 |
3,251 |
3,170 |
3,665 |
|
|
№ 1 |
|||||||||
|
3,314 |
3,278 |
3,262 |
3,292 |
3,332 |
3,397 |
3,487 |
3,563 |
||
|
№ 2 |
|||||||||
|
1,045 |
1,162 |
1,264 |
1,172 |
1,070 |
0,898 |
0,656 |
0,344 |
||
|
№ 3 |
|||||||||
|
6,715 |
6,735 |
6,750 |
6,741 |
6,645 |
6,639 |
6,647 |
6,612 |
||
|
№ 4 |
|||||||||
|
2,325 |
2,515 |
2,638 |
2,700 |
2,696 |
2,626 |
2,491 |
2,291 |
||
|
№ 5 |
|||||||||
|
1.752 |
1,762 |
1,777 |
1,797 |
1,821 |
1,850 |
1,884 |
1,944 |
||
|
№ 6 |
|||||||||
|
1,924 |
1,710 |
1,525 |
1,370 |
1,264 |
1,190 |
1,148 |
1,127 |
||
|
№ 7 |
|||||||||
|
1,025 |
1,144 |
1,336 |
1,419 |
1,479 |
1,530 |
1,568 |
1,248 |
||
|
№ 8 |
|||||||||
|
5,785 |
5,685 |
5,605 |
5,545 |
5,505 |
5,480 |
5,495 |
5,510 |
||
|
№ 9 |
|||||||||
|
4,052 |
4,092 |
4,152 |
4,234 |
4,338 |
4,468 |
4,599 |
LUCRARE DE CURS Aproximarea unei funcții prin metoda celor mai mici pătrate Introducere aproximarea empirică matematică Scopul cursului este aprofundarea cunoștințelor de informatică, dezvoltarea și consolidarea abilităților de lucru cu procesorul de foi de calcul Microsoft Excel și MathCAD. Aplicația lor pentru rezolvarea problemelor cu ajutorul unui calculator din domeniul de studiu legat de cercetare. În fiecare sarcină sunt formulate condițiile problemei, datele inițiale, formularul de emitere a rezultatelor, sunt indicate principalele dependențe matematice pentru rezolvarea problemei.Calculul de control vă permite să verificați funcționarea corectă a programului. Conceptul de aproximare este o expresie aproximativă a unor obiecte matematice (de exemplu, numere sau funcții) prin altele care sunt mai simple, mai convenabil de utilizat sau pur și simplu mai cunoscute. În cercetarea științifică, aproximarea este utilizată pentru a descrie, analiza, generaliza și folosi în continuare rezultatele empirice. După cum se știe, poate exista o conexiune exactă (funcțională) între valori, atunci când o valoare a argumentului corespunde unei anumite valori, și o conexiune (corelație) mai puțin precisă, când o anumită valoare a argumentului corespunde unei valori aproximative. sau un set de valori ale funcției care sunt mai mult sau mai puțin apropiate unele de altele. Când desfășurați cercetări științifice, procesați rezultatele unei observații sau experimente, de obicei trebuie să vă ocupați de a doua opțiune. Când se studiază dependențele cantitative ale diferiților indicatori, ale căror valori sunt determinate empiric, de regulă, există o oarecare variabilitate. Ea este determinată parțial de eterogenitatea obiectelor studiate ale naturii neînsuflețite și, mai ales, vie, parțial din cauza erorii de observare și prelucrare cantitativă a materialelor. Nu este întotdeauna posibilă eliminarea completă a ultimei componente; aceasta poate fi minimizată doar printr-o alegere atentă a unei metode de cercetare adecvate și a preciziei muncii. Specialiștii în domeniul automatizării proceselor și producțiilor tehnologice se ocupă cu o cantitate mare de date experimentale, pentru prelucrarea cărora se folosește un computer. Datele inițiale și rezultatele calculelor obținute pot fi prezentate sub formă de tabel folosind procesoare de foi de calcul (spreadsheets) și, în special, Excel. Cursurile de informatică permit studentului să-și consolideze și să dezvolte abilități de lucru cu ajutorul tehnologiilor informatice de bază în rezolvarea problemelor din domeniul activității profesionale.- un sistem de algebră computerizată din clasa sistemelor de proiectare asistată de calculator, axat pe pregătirea de documente interactive cu calcule și suport vizual, este ușor de utilizat și aplicat pentru lucrul în echipă. 1. Informatii generale Foarte des, mai ales atunci când se analizează datele empirice, devine necesar să se găsească în mod explicit relația funcțională dintre cantități XȘi la, care sunt obținute în urma măsurătorilor. Într-un studiu analitic al relației dintre două mărimi x și y, se fac o serie de observații și rezultă un tabel de valori: xx1 X1 XiXnda1 y1 yiYn Acest tabel este obținut de obicei în urma unor experimente în care X,(valoarea independentă) este stabilită de experimentator și y,obţinute ca urmare a experienţei. Prin urmare, aceste valori y,vor fi numite valori empirice sau experimentale. Există o relație funcțională între valorile x și y, dar forma sa analitică este de obicei necunoscută, așa că apare o sarcină practic importantă - găsirea unei formule empirice y=f (x; a 1, A 2,…, am ), (1) (Unde A1 , A2 ,…, Am- parametri), ale căror valori la x=x,ar diferi probabil puțin de valorile experimentale y, (i = 1,2,…, P). De obicei, indicați clasa de funcții (de exemplu, un set de liniară, putere, exponențială etc.) din care este selectată funcția f(x), iar apoi se determină cele mai bune valori ale parametrilor. Dacă în formula empirică (1) înlocuim inițiala X,atunci obținem valorile teoretice YTi= f (Xi; A 1, A 2……Am) , Unde i = 1,2,…, n. Diferențele yiT- lai, se numesc abateri si reprezinta distantele verticale fata de puncte Mila graficul funcţiei empirice. Conform metodei celor mai mici pătrate, cei mai buni coeficienți A1 , A2 ,…, Amsunt considerate cele pentru care suma abaterilor pătrate ale funcției empirice găsite de la valorile date ale funcției va fi minim. Să explicăm semnificația geometrică a metodei celor mai mici pătrate. Fiecare pereche de numere ( Xi, yi) din tabelul sursă definește un punct Mila suprafata XOY.Folosind formula (1) pentru diferite valori ale coeficienților A1 , A2 ,…, Ameste posibil să se construiască o serie de curbe care sunt grafice ale funcției (1). Problema este determinarea coeficienților A1 , A2 ,…, Amastfel încât suma pătratelor distanțelor verticale de la puncte Mi (Xi, yi) la graficul funcției (1) a fost cea mai mică (Fig. 1). Construcția unei formule empirice constă în două etape: aflarea formei generale a acestei formule și determinarea celor mai buni parametri ai acesteia. Dacă natura relaţiei dintre mărimile date x şi y, atunci forma dependenței empirice este arbitrară. Se acordă preferință formulelor simple, cu o bună acuratețe. Alegerea cu succes a unei formule empirice depinde în mare măsură de cunoștințele cercetătorului în domeniul subiectului, folosindu-se de el să indice clasa de funcții din considerente teoretice. De mare importanță este reprezentarea datelor obținute în sisteme de coordonate carteziene sau speciale (semilogaritmice, logaritmice etc.). După poziția punctelor, se poate ghici aproximativ forma generală a dependenței prin stabilirea asemănării dintre graficul construit și mostrele de curbe cunoscute. Determinarea celor mai bune cote A1 , A2,…, Amincluse în formula empirică produsă prin metode analitice binecunoscute. Pentru a găsi un set de coeficienți A1 , A2 …..Am, care livrează minimul funcției S definită prin formula (2), folosim condiția necesară pentru extremul unei funcții de mai multe variabile - egalitatea la zero a derivatelor parțiale. Ca urmare, obținem un sistem normal de determinare a coeficienților Ai(i = 1,2,…, m): Astfel, găsirea coeficienților Aireduce la sistemul de rezolvare (3). Acest sistem este simplificat dacă formula empirică (1) este liniară în raport cu parametrii Ai, atunci sistemul (3) va fi liniar. 1.1 Relație liniară Forma specifică a sistemului (3) depinde de clasa de formule empirice de la care căutăm dependența (1). În cazul unei relaţii liniare y=a1 + a2 Xsistemul (3) va lua forma: Acest sistem liniar poate fi rezolvat prin orice metodă cunoscută (metoda Gauss, iterații simple, formulele lui Cramer). 1.2 Dependență pătratică În cazul dependenţei pătratice y=a1 + a2 x + a3X 2sistemul (3) va lua forma: 1.3 Dependență exponențială În unele cazuri, ca formulă empirică, este luată o funcție în care coeficienți incerți intră neliniar. În acest caz, uneori problema poate fi liniarizată, adică. reduce la liniar. Printre astfel de dependențe se numără și dependența exponențială y=a1 *ea2x (6) unde un 1Și A 2, coeficienți nedefiniti. Linearizarea se realizează luând logaritmul de egalitate (6), după care obținem relația ln y = ln a 1+a 2X (7) Se notează ln lași ln AXrespectiv prin tȘi c, atunci dependența (6) poate fi scrisă ca t = a1 + a2 X, care ne permite să aplicăm formule (4) cu înlocuirea A1 pe cȘi lai pe ti 1.4 Elemente de teoria corelației Graficul dependenței funcționale restaurate y(x)conform rezultatelor măsurătorilor (x i, lai),i = 1,2, K, nnumită curbă de regresie. Pentru a verifica acordul curbei de regresie construită cu rezultatele experimentului, se introduc de obicei următoarele caracteristici numerice: coeficientul de corelație (dependența liniară), raportul de corelație și coeficientul de determinism. În acest caz, rezultatele sunt de obicei grupate și prezentate sub forma unui tabel de corelare. În fiecare celulă a acestui tabel sunt date numerele niJ - acele perechi (x, y), ale căror componente se încadrează în intervalele de grupare corespunzătoare pentru fiecare variabilă. Presupunând că lungimile intervalelor de grupare (pentru fiecare variabilă) sunt egale între ele, alegeți centrele x i(respectiv lai) din aceste intervale și numărul niJ- ca bază pentru calcule. Coeficientul de corelație este o măsură a relației liniare dintre variabile aleatoare dependente: arată cât de bine, în medie, una dintre variabile poate fi reprezentată ca o funcție liniară a celeilalte. Coeficientul de corelație se calculează prin formula: unde și, respectiv, sunt media aritmetică XȘi la. Coeficientul de corelație dintre variabilele aleatoare nu depășește în valoare absolută 1. Cu cât |р| la 1, cu atât este mai apropiată relația liniară dintre x și y. În cazul unei corelații neliniare, valorile medii condiționate sunt situate lângă linia curbă. În acest caz, se recomandă utilizarea unui raport de corelare ca caracteristică a forței conexiunii, a cărui interpretare nu depinde de tipul de dependență studiat. Raportul de corelație se calculează prin formula: Unde ni = , nf= , iar numărătorul caracterizează dispersia mediilor condiționate y, despre medie necondiționată y. Este mereu. Egalitate = 0 corespunde variabilelor aleatoare necorelate; = 1 dacă şi numai dacă există o relaţie funcţională exactă între yși x. În cazul unei relaţii liniare y din x, raportul de corelație coincide cu pătratul coeficientului de corelație. Valoare - ? 2 este folosit ca indicator al abaterii regresiei de la liniaritate. Raportul de corelație este o măsură a corelației y din X sub orice formă, dar nu poate oferi o idee despre gradul de aproximare a datelor empirice la o formă specială. Pentru a afla cât de exact curba construită reflectă datele empirice, este introdusă încă o caracteristică - coeficientul de determinism. Pentru a o descrie, luați în considerare următoarele cantități. este suma totală a pătratelor, unde este media. Putem demonstra următoarea egalitate Primul termen este egal cu Sres = și se numește suma reziduală a pătratelor. Caracterizează abaterea celor experimentale de la cele teoretice. Al doilea termen este egal cu Sreg = 2 și se numește suma de regresie a pătratelor și caracterizează răspândirea datelor. Este evident că următoarea egalitate S plin = S ost + S reg. Coeficientul de determinism este determinat de formula: Cu cât suma reziduală a pătratelor este mai mică în comparație cu suma totală a pătratelor, cu atât valoarea coeficientului de determinism este mai mare r2 , care arată cât de bine explică ecuația generată de analiza de regresie relațiile dintre variabile. Dacă este egal cu 1, atunci există o corelație completă cu modelul, adică. nu există nicio diferență între valorile y reale și estimate. În caz contrar, dacă coeficientul de determinism este 0, atunci ecuația de regresie nu reușește să prezică valorile y Coeficientul de determinism nu depășește întotdeauna raportul de corelație. În cazul în care egalitatea r 2 = atunci putem presupune că formula empirică construită reflectă cel mai exact datele empirice. 2. Enunțarea problemei 1. Folosind metoda celor mai mici pătrate, se aproximează funcția specificată în tabel a) un polinom de gradul I; b) un polinom de gradul II; c) dependenţă exponenţială. Pentru fiecare dependență, calculați coeficientul de determinism. Calculați coeficientul de corelație (numai în cazul a). Desenați o linie de tendință pentru fiecare dependență. Folosind funcția LINEST, calculați caracteristicile numerice ale dependenței de. Comparați calculele dvs. cu rezultatele obținute folosind funcția LINEST. Faceți o concluzie care dintre formulele obținute aproximează cel mai bine funcția. Scrieți un program într-unul dintre limbajele de programare și comparați rezultatele calculului cu cele obținute mai sus. 3. Date inițiale Funcția este dată în figura 1. 4. Calculul aproximărilor în foaia de calcul Excel Pentru calcule, este recomandabil să folosiți o foaie de calcul Microsoft Excel. Și aranjați datele așa cum se arată în Figura 2. Pentru asta intram: · în celulele A6:A30 introducem valorile xi . · în celulele B6:B30 introducem valorile ui . · în celula C6 introduceți formula =A6^ 2. · această formulă este copiată în celulele C7:C30. · În celula D6, introduceți formula =A6*B6. · această formulă este copiată în celulele D7:D30. · în celula F6, introduceți formula =A6^4. · această formulă este copiată în celulele F7:F30. · în celula G6 introducem formula =A6^2*B6. · această formulă este copiată în celulele G7:G30. · în celula H6, introduceți formula =LN(B6). · această formulă este copiată în celulele H7:H30. · în celula I6 introduceți formula =A6*LN(B6). · această formulă este copiată în celulele I7:I30. Facem următorii pași folosind autosumarea · în celula A33, introduceți formula = SUM (A6: A30). · în celula B33, introduceți formula = SUM (B6: B30). · în celula C33, introduceți formula = SUM (C6: C30). · în celula D33, introduceți formula = SUM (D6: D30). · în celula E33, introduceți formula =SUM (E6:E30). · în celula F33, introduceți formula = SUM (F6: F30). · în celula G33, introduceți formula = SUM (G6: G30). · în celula H33, introduceți formula = SUM (H6: H30). · în celula I33 introduceți formula = SUM (I6: I30). Aproximăm funcția y=f(x) funcție liniară y=a1 + a2X. Pentru a determina coeficienții a 1si a 2folosim sistemul (4). Folosind totalurile din Tabelul 2, situat în celulele A33, B33, C33 și D33, scriem sistemul (4) ca rezolvând care, obținem a 1= -24,7164 și a2 = 11,63183 Astfel, aproximarea liniară are forma y= -24,7164 + 11,63183x (12) Sistemul (11) a fost rezolvat folosind Microsoft Excel. Rezultatele sunt prezentate în Figura 3: În tabel, celulele A38:B39 conțin formula (=NBR (A35:B36)). Celulele E38:E39 conțin formula (=MULTI(A38:B39, C35:C36)). În continuare, aproximăm funcția y=f(x) funcție pătratică y=a1 + a2 x + a3 X2. Pentru a determina coeficienții a 1, A 2si a 3folosim sistemul (5). Folosind totalurile din Tabelul 2, situat în celulele A33, B33, C33, D33, E33, F33 și G33, scriem sistemul (5) ca: Rezolvând care, obținem a 1= 1,580946, a 2= -0,60819 și a3 = 0,954171 (14) Astfel, aproximarea pătratică are forma: y \u003d 1,580946 -0,60819x + 0,954171 x2 Sistemul (13) a fost rezolvat folosind Microsoft Excel. Rezultatele sunt prezentate în Figura 4. În tabel, celulele A46:C48 conțin formula (=NBR (A41:C43)). Celulele F46:F48 conțin formula (=MULTI(A41:C43, D46:D48)). Acum aproximăm funcția y=f(x) funcție exponențială y=a1 ea2x. Pentru a determina coeficienții A1 Și A2 luați logaritmul valorilor yiși folosind totalurile din tabelul 2, situat în celulele A26, C26, H26 și I26, obținem sistemul: Unde с = ln(a1 ). Rezolvarea sistemului (10) găsim c =0,506435, a2 = 0.409819. După potențare, obținem a1 = 1,659365. Astfel, aproximarea exponențială are forma y = 1,659365*e0,4098194x Sistemul (15) a fost rezolvat folosind Microsoft Excel. Rezultatele sunt prezentate în Figura 5. În tabel, celulele A55:B56 conțin formula (=NBR (A51:B52)). Celulele E54:E56 conțin formula (=MULTIPLE(A51:B52, C51:C52)). Celula E56 conține formula =EXP(E54). Calculați media aritmetică a lui x și y folosind formulele: Rezultatele calculului x și yInstrumentele Microsoft Excel sunt prezentate în Figura 6. Celula B58 conține formula =A33/25. Celula B59 conține formula =B33/25. masa 2 Să explicăm cum este compilat tabelul din Figura 7. Celulele A6:A33 și B6:B33 sunt deja completate (vezi Figura 2). · în celula J6, introduceți formula =(A6-$B$58)*(B6-$B$59). · această formulă este copiată în celulele J7:J30. · în celula K6, introduceți formula =(A6-$B$58)^ 2. · această formulă este copiată în celulele K7:K30. · în celula L6, introduceți formula =(B1-$B$59)^2. · această formulă este copiată în celulele L7:L30. · în celula M6 introduceți formula =($E$38+$E$39*A6-B6)^2. · această formulă este copiată în celulele M7:M30. · în celula N6, introduceți formula =($F$46 +$F$47*A6 +$F$48*A6 L6-B6)^2. · această formulă este copiată în celulele N7:N30. · în celula O6, introduceți formula =($E$56*EXP ($E$55*A6) - B6)^2. · această formulă este copiată în celulele O7:O30. Următorii pași se fac folosind autosumarea. · în celula J33, introduceți formula =CYMM (J6:J30). · în celula K33, introduceți formula = SUM (K6: K30). · în celula L33, introduceți formula =CYMM (L6:L30). · în celula M33 introduceți formula = SUM (M6: M30). · în celula N33 introduceți formula = SUM (N6: N30). · în celula O33, introduceți formula = SUM (06:030). Acum să calculăm coeficientul de corelație folosind formula (8) (numai pentru aproximarea liniară) și coeficientul de determinism folosind formula (10). Rezultatele calculelor folosind Microsoft Excel sunt prezentate în Figura 7. În tabelul 8, celula B61 conține formula =J33/(K33*L33^(1/2). Celula B62 conține formula =1 - M33/L33. Celula B63 conține formula =1 - N33/L33. Celula B64 conține formula =1 - O33/L33. O analiză a rezultatelor calculului arată că aproximarea pătratică descrie cel mai bine datele experimentale. 4.1 Reprezentare grafică în Excel Să selectăm celulele A1:A25, după care ne vom întoarce la expertul diagramă. Să alegem un grafic de dispersie. După ce diagrama este construită, faceți clic dreapta pe linia diagramei și alegeți să adăugați o linie de tendință (liniară, exponențială, putere și respectiv polinom de gradul doi). Graficul de aproximare liniară Graficul de aproximare cuadratică Graficul de potrivire exponențială. 5. Aproximarea unei funcții folosind MathCAD Aproximarea datelor luând în considerare parametrii lor statistici se referă la probleme de regresie. Acestea apar de obicei în timpul prelucrării datelor experimentale obținute ca urmare a măsurătorilor proceselor sau fenomenelor fizice care sunt de natură statistică (cum ar fi măsurători în radiometrie și geofizică nucleară), sau la un nivel ridicat de interferență (zgomot). Sarcina analizei de regresie este selectarea formulelor matematice care descriu cel mai bine datele experimentale. .1 Regresia liniară Regresia liniară în sistemul Mathcad este efectuată pe vectorii argumentului Xși lecturi Y functii: interceptare (x, y)- calculează parametrul dar1 , deplasarea verticală a dreptei de regresie (vezi fig.) panta (x, y)- calculează parametrul A2 , panta dreptei de regresie (vezi figura) y(x) = a1+a2*x Funcţie corr(y, y(x))calculează Coeficientul de corelație al lui Pearson.Cu cât este mai aproape de el 1, cu atât datele procesate corespund mai precis unei relații liniare (vezi fig.) .2 Regresia polinomială Regresia polinomială unidimensională cu un grad arbitrar n al polinomului și cu coordonate ale eșantionului arbitrare în Mathcad este realizată de funcțiile: regres (x, y, n)- calculează un vector S,care conţine coeficienţii aipolinom n gradul; Valorile coeficientului aipoate fi extras din vector Sfuncţie submatrice (S, 3, lungime(S) - 1, 0, 0). Valorile obținute ale coeficienților sunt utilizate în ecuația de regresie y(x) = a1+a2*x+a3*x2 (vezi poza.) .3 Regresia neliniară Pentru formulele de aproximare tipice simple, sunt furnizate un număr de funcții de regresie neliniară, în care parametrii funcției sunt selectați de programul Mathcad. Printre acestea se numără și funcția expfit(x, y, s),care returnează un vector care conține coeficienții a1, a2Și a3functie exponentiala y(x) = a1 ^exp (a2x) + a3.V vector Sse introduc valorile inițiale ale coeficienților a1, a2Și a3prima aproximare. Concluzie O analiză a rezultatelor calculului arată că aproximarea liniară descrie cel mai bine datele experimentale. Rezultatele obținute cu ajutorul programului MathCAD se potrivesc complet cu valorile obținute folosind Excel. Aceasta indică corectitudinea calculelor. Bibliografie
ÎndrumareAi nevoie de ajutor pentru a învăța un subiect?
Experții noștri vă vor consilia sau vă vor oferi servicii de îndrumare pe subiecte care vă interesează. Aproximarea datelor experimentale este o metodă bazată pe înlocuirea datelor obținute experimental cu o funcție analitică care trece cel mai aproape sau coincide în punctele nodale cu valorile inițiale (date obținute în timpul experimentului sau experimentului). În prezent, există două moduri de a defini o funcție analitică: Prin construirea unui polinom de interpolare de n grade care trece direct prin toate punctele o gamă dată de date. În acest caz, funcția de aproximare este reprezentată ca: un polinom de interpolare în forma Lagrange sau un polinom de interpolare în forma Newton. Construind un polinom de aproximare de n grade care trece aproape de puncte din matricea de date dată. Astfel, funcția de aproximare netezește toate zgomotele (sau erorile) aleatorii care pot apărea în timpul experimentului: valorile măsurate în timpul experimentului depind de factori aleatori care fluctuează în funcție de propriile legi aleatorii (erori de măsurare sau instrumente, inexactitate sau experimentale). erori). În acest caz, funcția de aproximare este determinată prin metoda celor mai mici pătrate. Metoda celor mai mici pătrate(în literatura engleză Ordinary Least Squares, MCO) este o metodă matematică bazată pe definiția unei funcții de aproximare, care este construită în cea mai apropiată apropiere de puncte dintr-o serie dată de date experimentale. Proximitatea funcțiilor inițiale și de aproximare F(x) este determinată de o măsură numerică și anume: suma abaterilor pătrate ale datelor experimentale de la curba de aproximare F(x) ar trebui să fie cea mai mică. Curba de potrivire construită prin metoda celor mai mici pătrate Se folosește metoda celor mai mici pătrate: Să rezolve sisteme de ecuații supradeterminate când numărul de ecuații depășește numărul de necunoscute; Pentru a căuta o soluție în cazul sistemelor de ecuații neliniare obișnuite (nu supradeterminate); Pentru aproximarea valorilor punctuale printr-o funcție de aproximare. Funcția de aproximare prin metoda celor mai mici pătrate este determinată din condiția sumei minime a abaterilor pătrate a funcției de aproximare calculată dintr-o serie dată de date experimentale. Acest criteriu al metodei celor mai mici pătrate se scrie ca următoarea expresie:
Valorile funcției de aproximare calculate la punctele nodale, Matrice specificată de date experimentale la punctele nodale. Un criteriu pătratic are o serie de proprietăți „bune”, cum ar fi diferențiabilitatea, oferind o soluție unică la problema de aproximare cu funcții de aproximare polinomială. În funcție de condițiile problemei, funcția de aproximare este un polinom de gradul m Gradul funcției de aproximare nu depinde de numărul de puncte nodale, dar dimensiunea acesteia trebuie să fie întotdeauna mai mică decât dimensiunea (numărul de puncte) a matricei date de date experimentale.
∙ Dacă gradul funcției de aproximare este m=1, atunci aproximăm funcția tabelă cu o dreaptă (regresie liniară). ∙ Dacă gradul funcției de aproximare este m=2, atunci aproximăm funcția tabelă cu o parabolă pătratică (aproximare pătratică). ∙ Dacă gradul funcției de aproximare este m=3, atunci aproximăm funcția tabelă cu o parabolă cubică (aproximație cubică). În cazul general, când este necesară construirea unui polinom de aproximare de gradul m pentru valori tabelare date, condiția pentru suma minimă a abaterilor pătrate asupra tuturor punctelor nodale este rescrisă în următoarea formă:
Numărul de valori specificate din tabel. O condiție necesară pentru existența unui minim al unei funcții este egalitatea cu zero a derivatelor sale parțiale în raport cu variabilele necunoscute
Să transformăm sistemul liniar de ecuații rezultat: deschideți parantezele și mutați termenii liberi în partea dreaptă a expresiei. Ca urmare, sistemul rezultat de expresii algebrice liniare va fi scris în următoarea formă:
Acest sistem de expresii algebrice liniare poate fi rescris sub formă de matrice:
Ca urmare, s-a obținut un sistem de ecuații liniare de dimensiunea m + 1, care constă din m + 1 necunoscute. Acest sistem poate fi rezolvat folosind orice metodă de rezolvare a ecuațiilor algebrice liniare (de exemplu, metoda Gauss). Ca urmare a soluției, se vor găsi parametri necunoscuți ai funcției de aproximare care furnizează suma minimă a abaterilor pătrate ale funcției de aproximare față de datele originale, adică. cea mai bună aproximare pătratică posibilă. Trebuie amintit că, dacă chiar și o valoare a datelor inițiale se modifică, toți coeficienții își vor schimba valorile, deoarece sunt complet determinați de datele inițiale. Aproximarea datelor inițiale prin dependență liniară (regresie liniara) Ca exemplu, luați în considerare metoda de determinare a funcției de aproximare, care este dată ca o relație liniară. În conformitate cu metoda celor mai mici pătrate, condiția pentru suma minimă a abaterilor pătrate se scrie după cum urmează: Coordonatele punctelor nodale ale tabelului; Coeficienți necunoscuți ai funcției de aproximare, care este dat ca relație liniară. O condiție necesară pentru existența unui minim al unei funcții este egalitatea la zero a derivatelor sale parțiale în raport cu variabilele necunoscute. Ca rezultat, obținem următorul sistem de ecuații:
Să transformăm sistemul liniar de ecuații rezultat.
Rezolvăm sistemul rezultat de ecuații liniare. Coeficienții funcției de aproximare în forma analitică se determină după cum urmează (metoda lui Cramer):
Acești coeficienți asigură construcția unei funcții de aproximare liniare în conformitate cu criteriul de minimizare a sumei pătratelor funcției de aproximare din valori tabelare date (date experimentale). Algoritm pentru implementarea metodei celor mai mici pătrate 1. Date inițiale: Având în vedere o serie de date experimentale cu numărul de măsurători N Este dat gradul polinomului de aproximare (m). 2. Algoritm de calcul: 2.1. Se determină coeficienți pentru construirea unui sistem de ecuații cu dimensiune
Coeficienții sistemului de ecuații (partea stângă a ecuației)
Membri liberi ai sistemului de ecuații liniare (partea dreaptă a ecuației)
2.2. Formarea unui sistem de ecuații liniare cu dimensiunea .
2.3. Rezolvarea unui sistem de ecuații liniare pentru a determina coeficienții necunoscuți ai polinomului de aproximare de gradul m. 2.4 Determinarea sumei abaterilor pătrate ale polinomului de aproximare de la valorile inițiale pe toate punctele nodale
Valoarea găsită a sumei abaterilor pătrate este minimul posibil. Aproximare cu alte funcții Trebuie remarcat că atunci când se aproximează datele inițiale în conformitate cu metoda celor mai mici pătrate, o funcție logaritmică, o funcție exponențială și o funcție de putere sunt uneori folosite ca funcție de aproximare. Aproximarea jurnalului Luați în considerare cazul în care funcția de aproximare este dată de o funcție logaritmică de forma: | ||