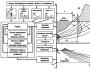
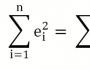Deneysel verilerin yaklaşıklığı. En küçük kareler yöntemi. Bir fonksiyonun en küçük kareler yöntemiyle yaklaştırılması En küçük kareler yönteminin yaklaşık olarak kullanılması
Hizalamadan sonra aşağıdaki formda bir fonksiyon elde ederiz: g (x) = x + 1 3 + 1 .
Bu verilere uygun parametreleri hesaplayarak doğrusal bir y = a x + b ilişkisi ile yaklaşabiliriz. Bunu yapmak için, sözde en küçük kareler yöntemini uygulamamız gerekecek. Ayrıca, deneysel verileri en iyi hangi çizginin hizalayacağını kontrol etmek için bir çizim yapmanız gerekecektir.
OLS tam olarak nedir (en küçük kareler yöntemi)
Yapmamız gereken asıl şey, iki değişkenli F (a, b) = ∑ i = 1 n (yi - (axi + b)) 2'nin fonksiyonunun değerinin en küçük olacağı böyle doğrusal bağımlılık katsayılarını bulmaktır. . Başka bir deyişle, belirli a ve b değerleri için, sunulan verilerin ortaya çıkan düz çizgiden sapmalarının karelerinin toplamı minimum bir değere sahip olacaktır. En küçük kareler yönteminin anlamı budur. Örneği çözmek için tek yapmamız gereken iki değişkenli fonksiyonun ekstremumunu bulmak.
Katsayıları hesaplamak için formüller nasıl türetilir
Katsayıları hesaplamak için formüller türetmek için, iki değişkenli bir denklem sistemi oluşturmak ve çözmek gerekir. Bunu yapmak için, F (a , b) = ∑ i = 1 n (y i - (a x i + b)) 2 ifadesinin a ve b'ye göre kısmi türevlerini hesaplar ve 0 ile eşitleriz.
δ F (a , b) δ a = 0 δ F (a , b) δ b = 0 ⇔ - 2 ∑ ben = 1 n (yi - (axi + b)) xi = 0 - 2 ∑ ben = 1 n ( yi - (eksen + b)) = 0 ⇔ bir ∑ ben = 1 nxi 2 + b ∑ ben = 1 nxi = ∑ ben = 1 nxiyia ∑ ben = 1 nxi + ∑ ben = 1 nb = ∑ ben = 1 nyi ⇔a ∑ ben = 1 nxi 2 + b ∑ ben = 1 nxi = ∑ ben = 1 nxiyia ∑ ben = 1 nxi + nb = ∑ ben = 1 nyi
Bir denklem sistemini çözmek için ikame veya Cramer yöntemi gibi herhangi bir yöntemi kullanabilirsiniz. Sonuç olarak en küçük kareler yöntemini kullanarak katsayıları hesaplayan formüller elde etmeliyiz.
n ∑ ben = 1 n x ben y ben - ∑ ben = 1 n x ben ∑ ben = 1 n y ben n ∑ ben = 1 n - ∑ ben = 1 n x ben 2 b = ∑ ben = 1 n y ben - bir ∑ ben = 1 n x ben n
Fonksiyonun ait olduğu değişkenlerin değerlerini hesapladık.
F (a , b) = ∑ ben = 1 n (y ben - (a x ben + b)) 2 minimum değeri alacaktır. Üçüncü paragrafta, neden böyle olduğunu kanıtlayacağız.
Bu en küçük kareler yönteminin pratikteki uygulamasıdır. a parametresini bulmak için kullanılan formülü, ∑ i = 1 n x ben , ∑ ben = 1 n y ben , ∑ ben = 1 n x ben y ben , ∑ ben = 1 n x ben 2 'yi ve parametreyi içerir.
n - deneysel veri miktarını belirtir. Her miktarı ayrı ayrı hesaplamanızı tavsiye ederiz. Katsayı değeri b, a'dan hemen sonra hesaplanır.
Orijinal örneğe geri dönelim.
örnek 1
Burada n eşittir beş var. Katsayı formüllerinde yer alan gerekli miktarları hesaplamayı daha kolay hale getirmek için tabloyu dolduruyoruz.
| ben = 1 | ben = 2 | ben = 3 | ben = 4 | ben = 5 | ∑ ben = 1 5 | |
| x ben | 0 | 1 | 2 | 4 | 5 | 12 |
| ben | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 | 12 , 9 |
| x ben y ben | 0 | 2 , 4 | 5 , 2 | 11 , 2 | 15 | 33 , 8 |
| x ben 2 | 0 | 1 | 4 | 16 | 25 | 46 |
Çözüm
Dördüncü satır, her bir i için ikinci satırdaki değerlerin üçüncünün değerleriyle çarpılmasıyla elde edilen verileri içerir. Beşinci satır, ikinci karedeki verileri içerir. Son sütun, tek tek satırların değerlerinin toplamını gösterir.
İhtiyacımız olan a ve b katsayılarını hesaplamak için en küçük kareler yöntemini kullanalım. Bunu yapmak için, son sütundan istenen değerleri değiştirin ve toplamları hesaplayın:
n ∑ ben = 1 nxiyi - ∑ ben = 1 nxi ∑ ben = 1 nyin ∑ ben = 1 n - ∑ ben = 1 nxi 2 b = ∑ ben = 1 nyi - bir ∑ ben = 1 nxin ⇒ a = 5 33 , 8 - 12 12, 9 5 46 - 12 2 b = 12, 9 - a 12 5 ⇒ a ≈ 0, 165 b ≈ 2, 184
İstenen yaklaşık düz çizginin y = 0 , 165 x + 2 , 184 gibi görüneceğini anladık. Şimdi hangi satırın verilere en iyi şekilde yaklaşacağını belirlememiz gerekiyor - g (x) = x + 1 3 + 1 veya 0 , 165 x + 2 , 184 . En küçük kareler yöntemini kullanarak bir tahmin yapalım.
Hatayı hesaplamak için, σ 1 = ∑ i = 1 n (yi - (axi + bi)) 2 ve σ 2 = ∑ i = 1 n (yi - g (xi)) 2 , minimum değer daha uygun bir satıra karşılık gelecektir.
σ 1 = ∑ ben = 1 n (yi - (eksen + bi)) 2 = = ∑ ben = 1 5 (yi - (0 , 165 xi + 2 , 184)) 2 ≈ 0 , 019 σ 2 = ∑ ben = 1 n (yi - g (xi)) 2 = = ∑ ben = 1 5 (yi - (xi + 1 3 + 1)) 2 ≈ 0 , 096
Yanıt vermek:σ 1'den beri< σ 2 , то прямой, наилучшим образом аппроксимирующей исходные данные, будет
y = 0 , 165 x + 2 , 184 .
En küçük kareler yöntemi, grafik şekilde açıkça gösterilmiştir. Kırmızı çizgi g (x) = x + 1 3 + 1 düz çizgisini, mavi çizgi y = 0, 165 x + 2, 184'ü gösterir. Ham veriler pembe noktalarla işaretlenmiştir.
Bu türden tam olarak yaklaşımlara neden ihtiyaç duyulduğunu açıklayalım.
Veri yumuşatma gerektiren problemlerde ve ayrıca verilerin enterpolasyonu veya ekstrapolasyonu gereken problemlerde kullanılabilirler. Örneğin, yukarıda tartışılan problemde, x = 3 veya x = 6'da gözlemlenen y niceliğinin değeri bulunabilir. Bu tür örneklere ayrı bir makale ayırdık.
LSM yönteminin kanıtı
Fonksiyonun hesaplanan a ve b için minimum değeri alması için, belirli bir noktada F (a, b) = ∑ i = 1 n ( yi - (axi + b)) 2 pozitif tanımlı olsun. Nasıl görünmesi gerektiğini size gösterelim.
Örnek 2
Aşağıdaki formun ikinci dereceden bir diferansiyeline sahibiz:
d 2 F (a ; b) = δ 2 F (a ; b) δ bir 2 d 2 a + 2 δ 2 F (a ; b) δ bir δ bdadb + δ 2 F (a ; b) δ b 2 d 2b
Çözüm
δ 2 F (a ; b) δ bir 2 = δ δ F (a ; b) δ bir δ a = = δ - 2 ∑ ben = 1 n (yi - (eksen + b)) xi δ bir = 2 ∑ ben = 1 n (xi) 2 δ 2 F (a ; b) δ bir δ b = δ δ F (a ; b) δ bir δ b = = δ - 2 ∑ ben = 1 n (yi - (axi + b) ) xi δ b = 2 ∑ ben = 1 nxi δ 2 F (a ; b) δ b 2 = δ δ F (a ; b) δ b δ b = δ - 2 ∑ ben = 1 n (yi - (axi + b)) δ b = 2 ∑ ben = 1 n (1) = 2 n
Başka bir deyişle, şu şekilde yazılabilir: d 2 F (a ; b) = 2 ∑ ben = 1 n (x i) 2 d 2 a + 2 2 ∑ x ben ben = 1 n d a d b + (2 n) d 2 b .
M = 2 ∑ i = 1 n (x i) 2 2 ∑ i = 1 n x ben 2 ∑ ben = 1 n x ben 2 n şeklinde ikinci dereceden bir matris elde ettik.
Bu durumda, bireysel elemanların değerleri a ve b'ye bağlı olarak değişmeyecektir. Bu matris pozitif tanımlı mı? Bu soruyu cevaplamak için açısal minörlerin pozitif olup olmadığını kontrol edelim.
Birinci mertebeden açısal minör hesaplayın: 2 ∑ i = 1 n (x i) 2 > 0 . x i noktaları çakışmadığı için eşitsizlik katıdır. Daha sonraki hesaplamalarda bunu göz önünde bulunduracağız.
İkinci dereceden açısal minörü hesaplıyoruz:
d e t (M) = 2 ∑ ben = 1 n (x ben) 2 2 ∑ ben = 1 n x ben 2 ∑ ben = 1 n x ben 2 n = 4 n ∑ ben = 1 n (x ben) 2 - ∑ ben = 1 n x ben 2
Bundan sonra, matematiksel tümevarım kullanarak n ∑ i = 1 n (x i) 2 - ∑ i = 1 n x i 2 > 0 eşitsizliğinin ispatına geçiyoruz.
- Bu eşitsizliğin keyfi n için geçerli olup olmadığını kontrol edelim. 2 alalım ve hesaplayalım:
2 ∑ ben = 1 2 (xi) 2 - ∑ ben = 1 2 xi 2 = 2 x 1 2 + x 2 2 - x 1 + x 2 2 = = x 1 2 - 2 x 1 x 2 + x 2 2 = x 1 + x 2 2 > 0
Doğru eşitliği elde ettik (eğer x 1 ve x 2 değerleri uyuşmuyorsa).
- Bu eşitsizliğin n için doğru olacağını varsayalım, yani. n ∑ ben = 1 n (x ben) 2 - ∑ ben = 1 n x ben 2 > 0 – doğru.
- Şimdi n + 1'in geçerliliğini ispatlayalım, yani. (n + 1) ∑ ben = 1 n + 1 (xi) 2 - ∑ ben = 1 n + 1 xi 2 > 0 ise n ∑ ben = 1 n (xi) 2 - ∑ ben = 1 nxi 2 > 0 .
Hesaplıyoruz:
(n + 1) ∑ ben = 1 n + 1 (xi) 2 - ∑ ben = 1 n + 1 xi 2 = = (n + 1) ∑ ben = 1 n (xi) 2 + xn + 1 2 - ∑ ben = 1 nxi + xn + 1 2 = = n ∑ ben = 1 n (xi) 2 + n xn + 1 2 + ∑ ben = 1 n (xi) 2 + xn + 1 2 - - ∑ ben = 1 nxi 2 + 2 xn + 1 ∑ ben = 1 nxi + xn + 1 2 = = ∑ ben = 1 n (xi) 2 - ∑ ben = 1 nxi 2 + n xn + 1 2 - xn + 1 ∑ ben = 1 nxi + ∑ ben = 1 n (xi) 2 = = ∑ ben = 1 n (xi) 2 - ∑ ben = 1 nxi 2 + xn + 1 2 - 2 xn + 1 x 1 + x 1 2 + + xn + 1 2 - 2 xn + 1 x 2 + x 2 2 + . . . + xn + 1 2 - 2 xn + 1 x 1 + xn 2 = = n ∑ ben = 1 n (xi) 2 - ∑ ben = 1 nxi 2 + + (xn + 1 - x 1) 2 + (xn + 1 - x 2) 2 + . . . + (x n - 1 - x n) 2 > 0
Kıvrımlı parantezler içine alınmış ifade 0'dan büyük olacaktır (2. adımda varsaydığımıza göre) ve geri kalan terimler 0'dan büyük olacaktır çünkü bunların tümü sayının kareleridir. Eşitsizliği kanıtladık.
Yanıt vermek: bulunan a ve b, F (a, b) = ∑ i = 1 n (yi - (axi + b)) 2 fonksiyonunun en küçük değerine karşılık gelecektir, bu, bunların en küçük kareler yönteminin istenen parametreleri olduğu anlamına gelir (LSM).
Metinde bir hata fark ederseniz, lütfen vurgulayın ve Ctrl+Enter tuşlarına basın.
Belirli bir fonksiyonun daha basit olanlarla yaklaşık temsiline izin verdiği için birçok uygulaması vardır. LSM, gözlemlerin işlenmesinde son derece yararlı olabilir ve rastgele hatalar içeren diğer ölçümlerin sonuçlarından bazı miktarları tahmin etmek için aktif olarak kullanılır. Bu makalede, Excel'de en küçük kareler hesaplamalarının nasıl uygulanacağını öğreneceksiniz.
Sorunun belirli bir örnek üzerinde ifadesi
X ve Y'nin iki göstergesi olduğunu varsayalım. Ayrıca, Y, X'e bağlıdır. OLS, regresyon analizi açısından bizi ilgilendirdiği için (Excel'de yöntemleri yerleşik işlevler kullanılarak uygulanır), hemen devam etmeliyiz. belirli bir sorunu düşünmek için.
Öyleyse, X bir bakkalın metrekare cinsinden ölçülen satış alanı ve Y, milyonlarca ruble olarak tanımlanan yıllık ciro olsun.
Bir veya daha fazla perakende alanı varsa, mağazanın ne kadar ciroya (Y) sahip olacağına dair bir tahmin yapmak gerekir. Açıkça görülüyor ki, hipermarket tezgahtan daha fazla mal sattığı için Y = f (X) fonksiyonu artıyor.
Tahmin için kullanılan ilk verilerin doğruluğu hakkında birkaç söz
Diyelim ki n mağaza için verilerle oluşturulmuş bir tablomuz var.
Matematiksel istatistiklere göre, en az 5-6 nesne üzerindeki veriler incelenirse sonuçlar az çok doğru olacaktır. Ayrıca "anormal" sonuçlar kullanılamaz. Özellikle elit bir küçük butik, “masmarket” sınıfındaki büyük mağazaların cirosundan kat kat daha fazla ciroya sahip olabilir.
Yöntemin özü
Tablo verileri Kartezyen düzlemde M 1 (x 1, y 1), ... Mn (x n, y n) noktaları olarak görüntülenebilir. Şimdi problemin çözümü, grafiği M 1, M 2, .. Mn noktalarına mümkün olduğunca yakın geçen bir y = f (x) yaklaşık fonksiyonunun seçimine indirgenecektir.
Tabii ki, yüksek dereceli bir polinom kullanabilirsiniz, ancak bu seçeneğin uygulanması sadece zor değil, aynı zamanda tespit edilmesi gereken ana eğilimi yansıtmayacağından sadece yanlıştır. En makul çözüm, deneysel verilere en iyi yaklaşan y = ax + b düz çizgisini ve daha kesin olarak katsayıları - a ve b'yi aramaktır.
doğruluk puanı
Herhangi bir yaklaşım için, doğruluğunun değerlendirilmesi özellikle önemlidir. x ben noktası için fonksiyonel ve deneysel değerler arasındaki farkı (sapma) e ile belirtin, yani. e ben = y ben - f (x i).
Açıkçası, yaklaşıklığın doğruluğunu değerlendirmek için sapmaların toplamını kullanabilirsiniz, yani X'in Y'ye bağımlılığının yaklaşık bir temsili için düz bir çizgi seçerken, en küçük değerine sahip olanı tercih edilmelidir. ele alınan tüm noktalarda toplam ei. Ancak, her şey o kadar basit değil, çünkü olumlu sapmaların yanı sıra pratikte olumsuz olanlar da olacak.
Sapma modüllerini veya karelerini kullanarak problemi çözebilirsiniz. İkinci yöntem en yaygın kullanılanıdır. Regresyon analizi de dahil olmak üzere birçok alanda kullanılır (Excel'de uygulaması iki yerleşik işlev kullanılarak gerçekleştirilir) ve uzun süredir etkili olduğu kanıtlanmıştır.
en küçük kareler yöntemi
Excel'de, bildiğiniz gibi, seçilen aralıkta bulunan tüm değerlerin değerlerini hesaplamanıza izin veren yerleşik bir otomatik toplam işlevi vardır. Böylece (e 1 2 + e 2 2 + e 3 2 + ... e n 2) ifadesinin değerini hesaplamamıza hiçbir şey engel olmayacaktır.
Matematiksel gösterimde, bu şöyle görünür:

Karar başlangıçta düz bir çizgi kullanılarak yaklaşık olarak verildiğinden, elimizde:

Bu nedenle, X ve Y arasındaki belirli bir ilişkiyi en iyi tanımlayan düz bir çizgi bulma görevi, iki değişkenli bir fonksiyonun minimumunu hesaplamak anlamına gelir:

Bu, yeni a ve b değişkenlerine göre sıfır kısmi türevleri eşitlemeyi ve 2 bilinmeyenli iki denklemden oluşan ilkel bir sistemi çözmeyi gerektirir:

2'ye bölme ve toplamları manipüle etme gibi basit dönüşümlerden sonra şunu elde ederiz:

Örneğin, Cramer yöntemiyle çözerek, belirli a * ve b * katsayılarına sahip durağan bir nokta elde ederiz. Bu minimumdur, yani mağazanın belirli bir alan için hangi ciroya sahip olacağını tahmin etmek için, söz konusu örnek için bir regresyon modeli olan y = a * x + b * düz çizgisi uygundur. Tabii ki, kesin sonucu bulmanıza izin vermeyecek, ancak belirli bir alan için kredili bir mağaza satın almanın işe yarayıp yaramayacağı hakkında bir fikir edinmenize yardımcı olacaktır.
Excel'de en küçük kareler yöntemi nasıl uygulanır
Excel'in en küçük karelerin değerini hesaplama işlevi vardır. Şu forma sahiptir: TREND (bilinen Y değerleri; bilinen X değerleri; yeni X değerleri; sabit). Excel'de OLS hesaplama formülünü tablomuza uygulayalım.
Bunu yapmak için, Excel'de en küçük kareler yöntemi kullanılarak yapılan hesaplamanın sonucunun görüntülenmesi gereken hücreye “=” işaretini girin ve “TREND” işlevini seçin. Açılan pencerede, aşağıdakileri vurgulayarak uygun alanları doldurun:
- Y için bilinen değerler aralığı (bu durumda ciro verileri);
- aralık x 1 , …x n , yani perakende alanının boyutu;
- ve cironun boyutunu bulmanız gereken x'in bilinen ve bilinmeyen değerleri (çalışma sayfasındaki konumları hakkında bilgi için aşağıya bakın).
Ayrıca formülde mantıksal bir "Const" değişkeni vardır. Karşılık gelen alana 1 girerseniz, bu, b \u003d 0 olduğu varsayılarak hesaplamaların yapılması gerektiği anlamına gelir.
Birden fazla x değeri için tahmini bilmeniz gerekiyorsa, formülü girdikten sonra "Enter" tuşuna basmamalısınız, ancak "Shift" + "Control" + "Enter" ("Enter") kombinasyonunu yazmanız gerekir. ) klavyede.
Bazı özellikler
Regresyon analizine aptallar bile erişebilir. Bilinmeyen değişkenler dizisinin değerini tahmin etmeye yönelik Excel formülü - "TREND" - en küçük kareler yöntemini hiç duymamış olanlar tarafından bile kullanılabilir. Sadece çalışmasının bazı özelliklerini bilmek yeterlidir. Özellikle:
- Y değişkeninin bilinen değerlerinin aralığını bir satır veya sütunda düzenlerseniz, bilinen x değerlerine sahip her satır (sütun) program tarafından ayrı bir değişken olarak algılanır.
- TREND penceresinde x'i bilinen aralık belirtilmemişse, fonksiyonun Excel'de kullanılması durumunda, program onu, sayısı verilen değerlere sahip aralığa karşılık gelen tam sayılardan oluşan bir dizi olarak kabul edecektir y değişkeninin
- "Öngörülen" değerler dizisinin çıktısını almak için trend ifadesi bir dizi formülü olarak girilmelidir.
- Yeni x değerleri belirtilmemişse, TREND işlevi bunları bilinenlere eşit kabul eder. Belirtilmezlerse, dizi 1 bağımsız değişken olarak alınır; 2; 3; 4;…, zaten verilen parametreler y ile aralıkla orantılıdır.
- Yeni x değerlerini içeren aralık, verilen y değerlerine sahip aralıkla aynı veya daha fazla satır veya sütuna sahip olmalıdır. Başka bir deyişle, bağımsız değişkenlerle orantılı olmalıdır.
- Bilinen x değerlerine sahip bir dizi birden çok değişken içerebilir. Ancak, sadece birinden bahsediyorsak, verilen x ve y değerlerine sahip aralıkların orantılı olması gerekir. Birkaç değişken olması durumunda, verilen y değerlerine sahip aralığın bir sütuna veya bir satıra sığması gerekir.

TAHMİN işlevi
Birkaç fonksiyon kullanılarak gerçekleştirilir. Bunlardan birinin adı "ÖNCELİK". TREND'e benzer, yani en küçük kareler yöntemi kullanılarak yapılan hesaplamaların sonucunu verir. Ancak, yalnızca Y değerinin bilinmediği bir X için.
Artık, bir göstergenin gelecekteki değerinin değerini doğrusal bir eğilime göre tahmin etmenize olanak tanıyan aptallar için Excel formüllerini biliyorsunuz.
3. Yöntemi kullanarak fonksiyonların yaklaşıklığı
en küçük kareler
Deney sonuçları işlenirken en küçük kareler yöntemi kullanılır. yaklaşımlar (yaklaşımlar) deneysel veri analitik formül. Formülün özel biçimi, kural olarak, fiziksel değerlendirmelerden seçilir. Bu formüller şunlar olabilir:
![]()
![]()
ve diğerleri.
En küçük kareler yönteminin özü aşağıdaki gibidir. Ölçüm sonuçlarının tabloda sunulmasına izin verin:
|
tablo 4 |
||||
|
x n |
||||
|
y n |
||||
|
(3.1) |
nerede f bilinen bir fonksiyondur, 0 , 1 , …, m - değerleri bulunması gereken bilinmeyen sabit parametreler. En küçük kareler yönteminde, (3.1) fonksiyonunun deneysel bağımlılığa yaklaşımının en iyi olduğu kabul edilir.
|
(3.2) |
yani miktarlar a İstenen analitik fonksiyonun deneysel bağımlılıktan kare sapmaları minimum olmalıdır .
işlevi olduğunu unutmayın Q isminde viskoz olmayan.

tutarsızlıktan beri

o zaman bir minimumu vardır. Birkaç değişkenli bir fonksiyonun minimumu için gerekli bir koşul, bu fonksiyonun parametrelere göre tüm kısmi türevlerinin sıfıra eşit olmasıdır. Böylece, yaklaşıklık fonksiyonunun (3.1) parametrelerinin en iyi değerlerini, yani bu değerlerin bulunması Q = Q (a 0 , a 1 , …, bir m ) minimumdur, denklem sistemini çözmeye indirgenir:
|
(3.3) |
En küçük kareler yöntemine aşağıdaki geometrik yorum verilebilir: belirli bir türdeki sonsuz bir çizgi ailesi arasında, deneysel noktaların koordinatlarındaki kare farklarının ve noktaların karşılık gelen koordinatlarının toplamının olduğu bir çizgi bulunur. Bu doğrunun denklemi ile bulunan en küçük olacaktır.
Doğrusal bir fonksiyonun parametrelerini bulma
Deneysel verilerin doğrusal bir fonksiyonla temsil edilmesine izin verin:
Bu tür değerlerin seçilmesi gerekmektedir. a ve B , hangi işlev için
|
(3.4) |
minimal olacaktır. (3.4) fonksiyonunun minimumu için gerekli koşullar denklem sistemine indirgenir:
|
|
Dönüşümlerden sonra, iki bilinmeyenli iki lineer denklem sistemi elde ederiz:
|
|
(3.5) |
hangisini çözerek, parametrelerin istenen değerlerini buluyoruz a ve B .
İkinci dereceden bir fonksiyonun parametrelerini bulma
Yaklaşım işlevi ikinci dereceden bir bağımlılık ise
sonra parametreleri a , b , c fonksiyonun minimum koşulundan bulun:
|
(3.6) |
(3.6) fonksiyonu için minimum koşullar denklem sistemine indirgenir:
|
|
Dönüşümlerden sonra, üç bilinmeyenli üç lineer denklem sistemi elde ederiz:
|
|
(3.7) |
de parametrelerin istenen değerlerini bulduğumuz çözme a, b ve c.
Örnek vermek . Deney sonucunda aşağıdaki değerler tablosu elde edilsin. x ve y :
|
tablo 5 |
||||||||
|
ben |
0,705 |
0,495 |
0,426 |
0,357 |
0,368 |
0,406 |
0,549 |
0,768 |
Deneysel verilere doğrusal ve ikinci dereceden fonksiyonlarla yaklaşmak gerekir.
Çözüm. Yaklaşım fonksiyonlarının parametrelerini bulmak, lineer denklem (3.5) ve (3.7) sistemlerini çözmeye indirgenir. Sorunu çözmek için bir elektronik tablo işlemcisi kullanıyoruz mükemmel.
1. İlk önce sayfa 1 ve 2'yi birbirine bağlarız. Deneysel değerleri girin x ben ve ben sütunlara A ve B, ikinci satırdan başlayarak (ilk satırda sütun başlıklarını koyarız). Daha sonra bu sütunların toplamlarını hesaplayıp onuncu sıraya koyuyoruz.
C–G sütunlarında sırasıyla hesaplamayı ve toplamı yerleştirin
2. Sayfaları kancadan çıkarın, Sayfa 1'e doğrusal bağımlılık ve Sayfa 2'ye ikinci dereceden bağımlılık için diğer hesaplamalar benzer şekilde yapılacaktır.
3. Ortaya çıkan tablonun altında, bir katsayı matrisi ve serbest terimlerin bir sütun vektörü oluştururuz. Doğrusal denklem sistemini aşağıdaki algoritmaya göre çözelim:
Ters matrisi hesaplamak ve matrisleri çarpmak için kullanırız Usta fonksiyonlar ve fonksiyonlar MOBR Ve MUMNOZH.
4. H2 hücre bloğunda: H 9 elde edilen katsayılara dayanarak hesaplıyoruz yaklaşık değerler polinomben kireç., blok I 2: I 9 - sapmalar gün ben = ben tecrübe. - ben kireç., J sütununda - tutarsızlık:
Kullanılarak elde edilen ve oluşturulan tablolar Grafik Sihirbazları grafikler şekil 6, 7, 8'de gösterilmiştir.

Pirinç. 6. Doğrusal bir fonksiyonun katsayılarını hesaplama tablosu,
yaklaşma deneysel veri.

Pirinç. 7. İkinci dereceden bir fonksiyonun katsayılarını hesaplama tablosu,
yaklaşmadeneysel veri.

Pirinç. 8. Yaklaşım sonuçlarının grafiksel gösterimi
deneysel veriler doğrusal ve ikinci dereceden fonksiyonlar.
Yanıt vermek. Deneysel veriler, doğrusal bağımlılık ile yaklaştırılmıştır. y = 0,07881 x + 0,442262 kalıntı ile Q = 0,165167 ve ikinci dereceden bağımlılık y = 3,115476 x 2 – 5,2175 x + 2,529631 kalıntı ile Q = 0,002103 .
Görevler. Tablo, doğrusal ve ikinci dereceden fonksiyonlar tarafından verilen fonksiyonu yaklaşık olarak hesaplayın.
|
Tablo 6 |
|||||||||
|
№0 |
x |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
|
y |
3,030 |
3,142 |
3,358 |
3,463 |
3,772 |
3,251 |
3,170 |
3,665 |
|
|
№ 1 |
|||||||||
|
3,314 |
3,278 |
3,262 |
3,292 |
3,332 |
3,397 |
3,487 |
3,563 |
||
|
№ 2 |
|||||||||
|
1,045 |
1,162 |
1,264 |
1,172 |
1,070 |
0,898 |
0,656 |
0,344 |
||
|
№ 3 |
|||||||||
|
6,715 |
6,735 |
6,750 |
6,741 |
6,645 |
6,639 |
6,647 |
6,612 |
||
|
№ 4 |
|||||||||
|
2,325 |
2,515 |
2,638 |
2,700 |
2,696 |
2,626 |
2,491 |
2,291 |
||
|
№ 5 |
|||||||||
|
1.752 |
1,762 |
1,777 |
1,797 |
1,821 |
1,850 |
1,884 |
1,944 |
||
|
№ 6 |
|||||||||
|
1,924 |
1,710 |
1,525 |
1,370 |
1,264 |
1,190 |
1,148 |
1,127 |
||
|
№ 7 |
|||||||||
|
1,025 |
1,144 |
1,336 |
1,419 |
1,479 |
1,530 |
1,568 |
1,248 |
||
|
№ 8 |
|||||||||
|
5,785 |
5,685 |
5,605 |
5,545 |
5,505 |
5,480 |
5,495 |
5,510 |
||
|
№ 9 |
|||||||||
|
4,052 |
4,092 |
4,152 |
4,234 |
4,338 |
4,468 |
4,599 |
DERS ÇALIŞMASI En küçük kareler yöntemiyle bir fonksiyonun yaklaşıklığı Tanıtım ampirik matematik yaklaşımı Ders çalışmasının amacı, bilgisayar bilimi bilgilerini derinleştirmek, Microsoft Excel ve MathCAD elektronik tablosuyla çalışma becerilerini geliştirmek ve pekiştirmektir. Araştırma ile ilgili konu alanından bir bilgisayar yardımıyla problem çözmeye yönelik uygulamaları. Her görevde, sorunun koşulları, ilk veriler, sonuç verme formu formüle edilir, sorunu çözmek için ana matematiksel bağımlılıklar belirtilir.Kontrol hesaplaması, programın doğru çalıştığını doğrulamanıza izin verir. Yaklaşım kavramı, bazı matematiksel nesnelerin (örneğin sayılar veya işlevler) daha basit, kullanımı daha kolay veya basitçe daha iyi bilinen diğerleri aracılığıyla yaklaşık bir ifadesidir. Bilimsel araştırmalarda, ampirik sonuçları tanımlamak, analiz etmek, genelleştirmek ve daha fazla kullanmak için yaklaşıklık kullanılır. Bilindiği gibi, argümanın bir değeri belirli bir değere karşılık geldiğinde değerler arasında tam (işlevsel) bir bağlantı ve argümanın belirli bir değeri yaklaşık bir değere karşılık geldiğinde daha az doğru (korelasyon) bir bağlantı olabilir. veya birbirine az çok yakın olan bazı fonksiyon değerleri kümesi. Bilimsel araştırma yaparken, bir gözlem veya deneyin sonuçlarını işlerken, genellikle ikinci seçenekle uğraşmak zorundasınız. Değerleri ampirik olarak belirlenen çeşitli göstergelerin nicel bağımlılıklarını incelerken, kural olarak, bazı değişkenlikler vardır. Kısmen, kısmen gözlem hatası ve malzemelerin kantitatif işlenmesi nedeniyle, incelenen cansız ve özellikle canlı doğanın nesnelerinin heterojenliği ile belirlenir. Son bileşeni tamamen ortadan kaldırmak her zaman mümkün değildir; ancak yeterli bir araştırma yönteminin ve işin doğruluğunun dikkatli bir şekilde seçilmesiyle en aza indirilebilir. Teknolojik süreçlerin ve üretimlerin otomasyonu alanındaki uzmanlar, işlenmesi için bir bilgisayarın kullanıldığı büyük miktarda deneysel veriyle ilgilenir. İlk veriler ve elde edilen hesaplama sonuçları, elektronik tablo işlemcileri (elektronik tablolar) ve özellikle Excel kullanılarak tablo şeklinde sunulabilir. Bilgisayar bilimlerinde kurs, öğrencinin mesleki faaliyet alanındaki problemlerin çözümünde temel bilgisayar teknolojilerinin yardımıyla çalışma becerilerini pekiştirmesine ve geliştirmesine olanak tanır. - hazırlık odaklı bilgisayar destekli tasarım sistemleri sınıfından bir bilgisayar cebir sistemi Hesaplamalar ve görsel destek ile etkileşimli belgelerden oluşan, ekip çalışması için kullanımı ve uygulaması kolaydır. 1. Genel bilgi Çok sık olarak, özellikle ampirik verileri analiz ederken, nicelikler arasındaki fonksiyonel ilişkiyi açıkça bulmak gerekli hale gelir. xVe de, ölçümler sonucunda elde edilir. İki nicelik x ve y arasındaki ilişkinin analitik bir çalışmasında, bir dizi gözlem yapılır ve sonuç bir değerler tablosu olur: xx1 x1 xixnyy1 y1 yiYn Bu tablo genellikle bazı deneyler sonucunda elde edilir. x,(bağımsız değer) deneyci tarafından belirlenir ve y,deneyim sonucu elde edilmiştir. Bu nedenle bu değerler y,ampirik veya deneysel değerler olarak adlandırılacaktır. X ve y değerleri arasında işlevsel bir ilişki vardır, ancak analitik formu genellikle bilinmemektedir, bu nedenle pratik olarak önemli bir görev ortaya çıkar - ampirik bir formül bulmak y=F (x; bir 1, a 2,…, ben ), (1) (nerede a1 , a2 ,…, am- parametreler), değerleri x=x,muhtemelen deneysel değerlerden çok az farklı olacaktır y, (i = 1,2,…, P). Genellikle, işlevin seçildiği işlev sınıfını (örneğin, bir dizi doğrusal, güç, üstel vb.) belirtin. f(x), ve ardından parametrelerin en iyi değerleri belirlenir. Ampirik formülde (1) ilkini değiştirirsek x,sonra teorik değerleri alırız YTi= f (xi; a 1, a 2……am) , nerede ben = 1,2,…, n. farklılıklar yiT-i, sapmalar olarak adlandırılır ve noktalardan dikey mesafeleri temsil eder. miampirik fonksiyonun grafiğine. En küçük kareler yöntemine göre en iyi katsayılar a1 , a2 ,…, ambulunan ampirik fonksiyonun kare sapmalarının toplamının fonksiyonun verilen değerlerinden olduğu kabul edilir. minimal olacaktır. En küçük kareler yönteminin geometrik anlamını açıklayalım. Her bir sayı çifti ( xi, yi) kaynak tablodan bir nokta tanımlar miyüzeyde XOY.Katsayıların farklı değerleri için formül (1) kullanma a1 , a2 ,…, am(1) fonksiyonunun grafikleri olan bir dizi eğri oluşturmak mümkündür. Sorun katsayıları belirlemektir. a1 , a2 ,…, amnoktalara olan düşey uzaklıkların karelerinin toplamı mi (xi, yi) fonksiyonunun (1) grafiğine göre en küçük olanıydı (Şekil 1). Ampirik bir formülün oluşturulması iki aşamadan oluşur: bu formülün genel biçimini bulmak ve en iyi parametrelerini belirlemek. Verilen miktarlar arasındaki ilişkinin doğası ise x ve y, o zaman ampirik bağımlılığın biçimi keyfidir. Doğruluğu iyi olan basit formüller tercih edilir. Ampirik bir formülün başarılı seçimi, büyük ölçüde araştırmacının, teorik düşüncelerden fonksiyon sınıfını gösterebileceği konu alanındaki bilgisine bağlıdır. Elde edilen verilerin Kartezyen veya özel koordinat sistemlerinde (semilogaritmik, logaritmik, vb.) temsili çok önemlidir. Noktaların konumuyla, oluşturulan grafik ve bilinen eğri örnekleri arasındaki benzerlik kurularak, bağımlılığın genel biçimi yaklaşık olarak tahmin edilebilir. En iyi oranların belirlenmesi a1 , a2,…, amiyi bilinen analitik yöntemlerle üretilen ampirik formüle dahil edilmiştir. Bir dizi katsayı bulmak için a1 , a2 …..am, formül (2) ile tanımlanan S fonksiyonunun minimumunu sağlayan, birkaç değişkenli bir fonksiyonun ekstremumu için gerekli koşulu kullanırız - kısmi türevlerin sıfıra eşitliği. Sonuç olarak, katsayıları belirlemek için normal bir sistem elde ederiz. ai(ben = 1,2,…, m): Böylece katsayıları bulmak aiçözme sistemine indirgenir (3). Ampirik formül (1) parametrelere göre doğrusal ise bu sistem basitleştirilir. ai, o zaman sistem (3) lineer olacaktır. 1.1 Doğrusal ilişki Sistemin (3) özel formu, bağımlılığı (1) aradığımız ampirik formüllerin sınıfına bağlıdır. Doğrusal bir ilişki olması durumunda y=a1 +a2 xsistem (3) şu şekli alacaktır: Bu lineer sistem bilinen herhangi bir yöntemle (Gauss yöntemi, basit yinelemeler, Cramer formülleri) çözülebilir. 1.2 İkinci dereceden bağımlılık İkinci dereceden bağımlılık durumunda y=a1 +a2 x + bir3x 2sistem (3) şu şekli alacaktır: 1.3 Üstel bağımlılık Bazı durumlarda, ampirik bir formül olarak, içine belirsiz katsayıların lineer olmayan bir şekilde girdiği bir fonksiyon alınır. Bu durumda bazen problem lineerleştirilebilir, yani. lineer olarak azaltın. Bu tür bağımlılıklar arasında üstel bağımlılık vardır. y=a1 * ea2x (6) burada bir 1Ve a 2, tanımsız katsayılar. Doğrusallaştırma, eşitliğin (6) logaritması alınarak elde edilir, ardından ilişkiyi elde ederiz. ln y = ln bir 1+a 2x (7) ln'yi belirtin deve ln axsırasıyla TVe C, o zaman bağımlılık (6) şu şekilde yazılabilir: t = bir1 +a2 x, bu, formülleri (4) değiştirme ile birlikte uygulamamıza izin verir. a1 üzerinde CVe deiüzerinde Ti 1.4 Korelasyon teorisinin unsurları Geri yüklenen fonksiyonel bağımlılığın grafiği y(x)ölçüm sonuçlarına göre (x i, dei),ben = 1.2, K, nregresyon eğrisi denir. Oluşturulan regresyon eğrisinin deneyin sonuçlarıyla uyumunu kontrol etmek için genellikle aşağıdaki sayısal özellikler tanıtılır: korelasyon katsayısı (doğrusal bağımlılık), korelasyon oranı ve determinizm katsayısı. Bu durumda, sonuçlar genellikle gruplandırılır ve bir korelasyon tablosu şeklinde sunulur. Bu tablonun her hücresinde sayılar verilmiştir. niJ - bu çiftler (x, y)bileşenleri, her bir değişken için karşılık gelen gruplama aralıkları içinde yer alan. Gruplama aralıklarının (her değişken için) uzunluklarının birbirine eşit olduğunu varsayarak, x merkezlerini seçin. i(sırasıyla dei) bu aralıkların sayısı ve niJ- hesaplamalar için temel olarak. Korelasyon katsayısı, bağımlı rastgele değişkenler arasındaki doğrusal ilişkinin bir ölçüsüdür: ortalama olarak, değişkenlerden birinin diğerinin doğrusal bir fonksiyonu olarak ne kadar iyi temsil edilebileceğini gösterir. Korelasyon katsayısı şu formülle hesaplanır: nerede ve sırasıyla aritmetik ortalamadır x Ve de. Rastgele değişkenler arasındaki korelasyon katsayısı mutlak değerde 1'i geçmez. 1'e, x ve arasındaki doğrusal ilişki ne kadar yakınsa y. Doğrusal olmayan bir korelasyon durumunda, koşullu ortalama değerler eğri çizginin yakınında bulunur. Bu durumda, yorumlanması incelenen bağımlılığın türüne bağlı olmayan bağlantının gücünün bir özelliği olarak bir korelasyon oranının kullanılması önerilir. Korelasyon oranı aşağıdaki formülle hesaplanır: nerede ni = , nF= ve pay, koşullu ortalamaların dağılımını karakterize eder y, koşulsuz ortalama hakkında y. Her zaman. eşitlik = 0, ilişkisiz rastgele değişkenlere karşılık gelir; = 1 arasında tam bir işlevsel ilişki varsa ve ancak y ve x. Doğrusal bir ilişki olması durumunda y x'ten korelasyon oranı, korelasyon katsayısının karesi ile çakışır. Değer - ? 2, regresyonun doğrusallıktan sapmasının bir göstergesi olarak kullanılır. Korelasyon oranı, korelasyonun bir ölçüsüdür y itibaren x herhangi bir biçimde, ancak ampirik verilerin özel bir forma yaklaşma derecesi hakkında bir fikir veremez. Oluşturulan eğrinin ampirik verileri ne kadar doğru yansıttığını bulmak için bir özellik daha tanıtıldı - determinizm katsayısı. Bunu tanımlamak için aşağıdaki miktarları göz önünde bulundurun. karelerin toplamı, ortalama nerede. Aşağıdaki eşitliği ispatlayabiliriz İlk terim Sres = eşittir ve kalan kareler toplamı olarak adlandırılır. Deneyin teorik olanlardan sapmasını karakterize eder. İkinci terim Sreg = 2'ye eşittir ve karelerin regresyon toplamı olarak adlandırılır ve verilerin yayılmasını karakterize eder. Aşağıdaki eşitlik S olduğu açıktır. tam = S ost + S reg. Determinizm katsayısı şu formülle belirlenir: Toplam kareler toplamına kıyasla artık kareler toplamı ne kadar küçükse, determinizm katsayısının değeri o kadar büyük olur. r2 Bu, regresyon analizi tarafından oluşturulan denklemin değişkenler arasındaki ilişkileri ne kadar iyi açıkladığını gösterir. 1'e eşitse, modelle tam bir korelasyon vardır, yani. gerçek ve tahmini y değerleri arasında fark yoktur. Aksi takdirde, determinizm katsayısı 0 ise, regresyon denklemi y değerlerini tahmin edemez. Determinizm katsayısı her zaman korelasyon oranını aşmaz. eşitliğinin sağlandığı durumda r 2 = o zaman oluşturulan ampirik formülün ampirik verileri en doğru şekilde yansıttığını varsayabiliriz. 2. Sorunun ifadesi 1. En küçük kareler yöntemini kullanarak, tabloda belirtilen fonksiyona yaklaşılır. a) birinci dereceden bir polinom; b) ikinci dereceden bir polinom; c) üstel bağımlılık. Her bağımlılık için determinizm katsayısını hesaplayın. Korelasyon katsayısını hesaplayın (sadece a durumunda). Her bağımlılık için bir eğilim çizgisi çizin. DOĞRU işlevini kullanarak, bağımlılığın sayısal özelliklerini hesaplayın. HATA işlevi kullanılarak elde edilen sonuçlarla hesaplamalarınızı karşılaştırın. Elde edilen formüllerden hangisinin fonksiyona en yakın olduğu sonucuna varın. Programlama dillerinden birinde bir program yazın ve hesaplama sonuçlarını yukarıda elde edilenlerle karşılaştırın. 3. İlk veriler Fonksiyon Şekil 1'de verilmiştir. 4. Excel tablosundaki yaklaşımların hesaplanması Hesaplamalar için bir Microsoft Excel elektronik tablosu kullanılması tavsiye edilir. Ve verileri Şekil 2'de gösterildiği gibi düzenleyin. Bunun için giriyoruz: · A6:A30 hücrelerinde xi değerlerini giriyoruz . · B6:B30 hücrelerinde kullanıcı arayüzünün değerlerini giriyoruz . · C6 hücresine =A6^ formülünü girin 2. · bu formül C7:C30 hücrelerine kopyalanır. · D6 hücresine =A6*B6 formülünü girin. · bu formül D7:D30 hücrelerine kopyalanır. · F6 hücresine =A6^4 formülünü girin. · bu formül F7:F30 hücrelerine kopyalanır. · G6 hücresine =A6^2*B6 formülünü giriyoruz. · bu formül G7:G30 hücrelerine kopyalanır. · H6 hücresine =LN(B6) formülünü girin. · bu formül H7:H30 hücrelerine kopyalanır. · I6 hücresine =A6*LN(B6) formülünü girin. · bu formül I7:I30 hücrelerine kopyalanır. Otomatik toplama kullanarak aşağıdaki adımları yapıyoruz · A33 hücresine = SUM (A6: A30) formülünü girin. · B33 hücresine = SUM (B6: B30) formülünü girin. · C33 hücresine = SUM (C6: C30) formülünü girin. · D33 hücresine = SUM (D6: D30) formülünü girin. · E33 hücresine =TOPLA (E6:E30) formülünü girin. · F33 hücresine = SUM (F6: F30) formülünü girin. · G33 hücresine = SUM (G6: G30) formülünü girin. · H33 hücresine = SUM (H6: H30) formülünü girin. · I33 hücresine = SUM (I6: I30) formülünü girin. fonksiyona yaklaşıyoruz y=f(x) doğrusal fonksiyon y=a1 +a2x. katsayıları belirlemek için a 1ve bir 2(4) sistemini kullanıyoruz. A33, B33, C33 ve D33 hücrelerinde bulunan Tablo 2'nin toplamlarını kullanarak, sistemi (4) olarak yazıyoruz. hangisini çözersek, bir 1= -24.7164 ve a2 = 11,63183 Böylece, doğrusal yaklaşım forma sahiptir y= -24.7164 + 11.63183x (12) Sistem (11) Microsoft Excel kullanılarak çözüldü. Sonuçlar Şekil 3'te sunulmuştur: Tabloda, A38:B39 hücreleri (=NBR (A35:B36)) formülünü içerir. E38:E39 hücreleri (=MULTI(A38:B39, C35:C36)) formülünü içerir. Ardından, işlevi yaklaşık olarak hesaplıyoruz y=f(x) ikinci dereceden fonksiyon y=a1 +a2 x + bir3 x2. katsayıları belirlemek için a 1, a 2ve bir 3(5) sistemini kullanıyoruz. A33, B33, C33, D33, E33, F33 ve G33 hücrelerinde bulunan Tablo 2'nin toplamlarını kullanarak, sistemi (5) şu şekilde yazıyoruz: Hangisini çözersek, bir 1= 1.580946, bir 2= -0.60819 ve a3 = 0,954171 (14) Böylece, ikinci dereceden yaklaşım şu şekildedir: y \u003d 1.580946 -0.60819x + 0.954171 x2 Sistem (13) Microsoft Excel kullanılarak çözüldü. Sonuçlar Şekil 4'te sunulmuştur. Tabloda, A46:C48 hücreleri (=NBR (A41:C43)) formülünü içerir. F46:F48 hücreleri (=MULTI(A41:C43, D46:D48)) formülünü içerir. Şimdi fonksiyona yaklaşıyoruz y=f(x) üstel fonksiyon y=a1 ea2x. Katsayıları belirlemek için a1 Ve a2 değerlerin logaritmasını al yive A26, C26, H26 ve I26 hücrelerinde bulunan tablo 2'nin toplamlarını kullanarak sistemi elde ederiz: nerede с = ln(a1 ). Çözme sistemi (10) buluyoruz c =0,506435, a2 = 0.409819. Güçlendirmeden sonra, a1 elde ederiz. = 1,659365. Böylece, üstel yaklaşım şu şekildedir: y = 1.659365*e0.4098194x Sistem (15) Microsoft Excel kullanılarak çözüldü. Sonuçlar Şekil 5'te gösterilmektedir. Tabloda, A55:B56 hücreleri (=NBR (A51:B52)) formülünü içerir. E54:E56 hücreleri şu formülü içerir (=ÇOKLU(A51:B52, C51:C52)). E56 hücresi, =EXP(E54) formülünü içerir. Aşağıdaki formülleri kullanarak x ve y'nin aritmetik ortalamasını hesaplayın: Hesaplama sonuçları x ve yMicrosoft Excel araçları Şekil 6'da gösterilmiştir. B58 hücresi =A33/25 formülünü içerir. B59 hücresi =B33/25 formülünü içerir. Tablo 2 Şekil 7'deki tablonun nasıl derlendiğini açıklayalım. A6:A33 ve B6:B33 hücreleri zaten doldurulmuştur (bkz. Şekil 2). · J6 hücresine =(A6-$B$58)*(B6-$B$59) formülünü girin. · bu formül J7:J30 hücrelerine kopyalanır. · K6 hücresine =(A6-$B$58)^ formülünü girin 2. · bu formül K7:K30 hücrelerine kopyalanır. · L6 hücresine =(B1-$B$59)^2 formülünü girin. · bu formül L7:L30 hücrelerine kopyalanır. · M6 hücresine =($E$38+$E$39*A6-B6)^2 formülünü girin. · bu formül M7:M30 hücrelerine kopyalanır. · N6 hücresine, =($F$46 +$F$47*A6 +$F$48*A6 L6-B6)^2 formülünü girin. · bu formül N7:N30 hücrelerine kopyalanır. · O6 hücresine, =($E$56*EXP ($E$55*A6) - B6)^2 formülünü girin. · bu formül O7:O30 hücrelerine kopyalanır. Sonraki adımlar otomatik toplama kullanılarak yapılır. · J33 hücresine =CYMM (J6:J30) formülünü girin. · K33 hücresine = SUM (K6: K30) formülünü girin. · L33 hücresine =CYMM (L6:L30) formülünü girin. · M33 hücresine = SUM (M6: M30) formülünü girin. · N33 hücresine = SUM (N6: N30) formülünü girin. · O33 hücresine = SUM (06:030) formülünü girin. Şimdi formül (8) kullanarak korelasyon katsayısını (sadece doğrusal yaklaşım için) ve formül (10) kullanarak determinizm katsayısını hesaplayalım. Microsoft Excel kullanılarak yapılan hesaplamaların sonuçları Şekil 7'de gösterilmektedir. Tablo 8'de, B61 hücresi =J33/(K33*L33^(1/2) formülünü içerir. B62 hücresi =1 - M33/L33 formülünü içerir. B63 hücresi =1 - N33/L33 formülünü içerir. B64 hücresi şunları içerir: formül =1 - O33/L33. Hesaplama sonuçlarının bir analizi, ikinci dereceden yaklaşımın deneysel verileri en iyi şekilde tanımladığını gösterir. 4.1 Excel'de Grafik Oluşturma A1:A25 hücrelerini seçelim, bundan sonra grafik sihirbazına döneceğiz. Bir dağılım grafiği seçelim. Grafik oluşturulduktan sonra, grafiğin çizgisine sağ tıklayın ve bir trend çizgisi eklemeyi seçin (sırasıyla doğrusal, üstel, kuvvet ve ikinci dereceden polinom). Doğrusal Yaklaşım Grafiği Kuadratik Yaklaşım Grafiği Üstel uyum grafiği. 5. MathCAD kullanarak bir fonksiyonun yaklaşıklığı İstatistiksel parametreleri dikkate alarak verilerin yaklaşıklığı, regresyon problemlerini ifade eder. Genellikle, doğası gereği istatistiksel olan (radyometri ve nükleer jeofizikteki ölçümler gibi) veya yüksek düzeyde parazit (gürültü) olan süreçlerin veya fiziksel olayların ölçümlerinin bir sonucu olarak elde edilen deneysel verilerin işlenmesi sırasında ortaya çıkarlar. Regresyon analizinin görevi, deneysel verileri en iyi tanımlayan matematiksel formüllerin seçilmesidir. .1 Doğrusal regresyon Mathcad sisteminde doğrusal regresyon, argümanın vektörleri üzerinde gerçekleştirilir. xve okumalar Y fonksiyonlar: kesişme (x, y)- parametreyi hesaplar fakat1 , regresyon çizgisinin dikey kayması (bkz. şek.) eğim (x, y)- parametreyi hesaplar a2 , regresyon çizgisinin eğimi (şekle bakın) y(x) = a1+a2*x İşlev doğru(y, y(x))hesaplar Pearson korelasyon katsayısı.O daha yakın 1, işlenen veriler daha doğru bir şekilde doğrusal bir ilişkiye karşılık gelir (bkz. Şek.) .2 Polinom Regresyon Mathcad'de keyfi bir polinom derecesi n ile ve rastgele örnek koordinatları olan tek boyutlu polinom regresyonu, fonksiyonlar tarafından gerçekleştirilir: gerileme(x, y, n)- bir vektör hesaplar S,katsayıları içeren benpolinom n inci derece; katsayı değerleri benvektörden çıkarılabilir Sişlev alt matris (S, 3, uzunluk(S) - 1, 0, 0). Katsayıların elde edilen değerleri regresyon denkleminde kullanılır y(x) = a1+a2*x+a3*x2 (resme bakın.) .3 Doğrusal olmayan regresyon Basit tipik yaklaşım formülleri için, fonksiyon parametrelerinin Mathcad programı tarafından seçildiği bir dizi doğrusal olmayan regresyon fonksiyonu sağlanmıştır. Bunlar arasında işlev exfit(x,y,s),katsayıları içeren bir vektör döndüren a1, a2Ve a3üstel fonksiyon y(x) = a1 ^exp (a2x) + a3.V vektör Skatsayıların ilk değerleri girilir a1, a2Ve a3ilk yaklaşım. Çözüm Hesaplama sonuçlarının bir analizi, doğrusal yaklaşımın deneysel verileri en iyi şekilde tanımladığını gösterir. MathCAD programı kullanılarak elde edilen sonuçlar, Excel kullanılarak elde edilen değerlerle tamamen örtüşmektedir. Bu, hesaplamaların doğruluğunu gösterir. bibliyografya
özel dersBir konuyu öğrenmek için yardıma mı ihtiyacınız var?
Uzmanlarımız, ilginizi çeken konularda tavsiyelerde bulunacak veya özel ders hizmetleri sunacaktır. Deneysel verilerin yaklaştırılması, deneysel olarak elde edilen verilerin, düğüm noktalarında ilk değerlerle (deney veya deney sırasında elde edilen veriler) en yakından geçen veya çakışan bir analitik fonksiyonla değiştirilmesine dayanan bir yöntemdir. Şu anda bir analitik işlevi tanımlamanın iki yolu vardır: geçen bir n-derece interpolasyon polinomu oluşturarak tüm noktalardan doğrudan verilen veri dizisi. Bu durumda, yaklaşıklık fonksiyonu şu şekilde temsil edilir: Lagrange formunda bir interpolasyon polinomu veya Newton formunda bir interpolasyon polinomu. geçen bir n-dereceli yaklaşım polinomu oluşturarak noktalara yakın verilen veri dizisinden. Böylece, yaklaşıklık işlevi, deney sırasında oluşabilecek tüm rastgele gürültüyü (veya hataları) düzeltir: deney sırasında ölçülen değerler, kendi rastgele yasalarına göre dalgalanan rastgele faktörlere bağlıdır (ölçüm veya cihaz hataları, yanlışlık veya deneysel). hatalar). Bu durumda, yaklaşım işlevi en küçük kareler yöntemiyle belirlenir. en küçük kareler yöntemi(İngilizce literatüründe Sıradan En Küçük Kareler, OLS), belirli bir deneysel veri dizisinden noktalara en yakın mesafede oluşturulan yaklaşık bir fonksiyonun tanımına dayanan matematiksel bir yöntemdir. F(x) başlangıç ve yaklaşıklık fonksiyonlarının yakınlığı, sayısal bir ölçü ile belirlenir, yani: deneysel verilerin F(x) yaklaşık eğrisinden sapmalarının karelerinin toplamı en küçük olmalıdır. En küçük kareler yöntemiyle oluşturulan uydurma eğrisi En küçük kareler yöntemi kullanılır: Denklem sayısı bilinmeyen sayısını aştığında, aşırı belirlenmiş denklem sistemlerini çözmek için; Sıradan (aşırı belirlenmemiş) doğrusal olmayan denklem sistemleri durumunda bir çözüm aramak; Bazı yaklaşım işlevleriyle nokta değerlerine yaklaşmak için. En küçük kareler yöntemiyle yaklaşıklık işlevi, belirli bir deneysel veri dizisinden hesaplanan yaklaşıklık işlevinin karelerinin minimum sapmalarının toplamı koşulundan belirlenir. En küçük kareler yönteminin bu kriteri aşağıdaki ifade olarak yazılır:
Düğüm noktalarında hesaplanan yaklaşıklık fonksiyonunun değerleri, Düğüm noktalarında belirtilen deneysel veri dizisi. İkinci dereceden bir kriter, türevlenebilirlik gibi bir dizi "iyi" özelliğe sahiptir ve polinom yaklaşma fonksiyonları ile yaklaşıklık problemine benzersiz bir çözüm sağlar. Problemin koşullarına bağlı olarak, yaklaşıklık fonksiyonu m dereceli bir polinomdur. Yaklaştırma fonksiyonunun derecesi düğüm noktalarının sayısına bağlı değildir, ancak boyutu her zaman verilen deneysel veri dizisinin boyutundan (nokta sayısı) daha az olmalıdır.
∙ Yaklaşım fonksiyonunun derecesi m=1 ise, o zaman tablo fonksiyonunu düz bir çizgiyle (doğrusal regresyon) tahmin ederiz. ∙ Yaklaşım fonksiyonunun derecesi m=2 ise, o zaman tablo fonksiyonuna ikinci dereceden bir parabol (kuadratik yaklaşım) ile yaklaşırız. ∙ Yaklaşım fonksiyonunun derecesi m=3 ise, o zaman tablo fonksiyonunu kübik bir parabolle (kübik yaklaşım) tahmin ederiz. Genel durumda, verilen tablo değerleri için m derecesinde yaklaşık bir polinom oluşturmak gerektiğinde, tüm düğüm noktaları üzerindeki minimum kare sapmaların toplamı için koşul aşağıdaki biçimde yeniden yazılır:
Belirtilen tablo değerlerinin sayısı. Bir fonksiyonun minimumunun varlığı için gerekli koşul, bilinmeyen değişkenlere göre kısmi türevlerinin sıfıra eşit olmasıdır.
Ortaya çıkan doğrusal denklem sistemini dönüştürelim: parantezleri açın ve serbest terimleri ifadenin sağ tarafına taşıyın. Sonuç olarak, elde edilen lineer cebirsel ifadeler sistemi aşağıdaki biçimde yazılacaktır:
Bu lineer cebirsel ifadeler sistemi matris biçiminde yeniden yazılabilir:
Sonuç olarak, m + 1 bilinmeyenlerden oluşan m + 1 boyutlu bir lineer denklem sistemi elde edildi. Bu sistem, lineer cebirsel denklemleri çözmek için herhangi bir yöntem kullanılarak çözülebilir (örneğin, Gauss yöntemi). Çözümün bir sonucu olarak, yaklaşıklık fonksiyonunun orijinal verilerden sapmalarının minimum kare toplamını sağlayan yaklaşıklık fonksiyonunun bilinmeyen parametreleri bulunacaktır, yani. mümkün olan en iyi ikinci dereceden yaklaşım. Unutulmamalıdır ki, ilk verinin bir değeri bile değişse, tüm katsayılar tamamen ilk veriler tarafından belirlendiği için değerlerini değiştirecektir. Doğrusal bağımlılık ile ilk verilerin yaklaşıklığı (doğrusal regresyon) Örnek olarak, doğrusal bir ilişki olarak verilen yaklaşık işlevi belirleme yöntemini düşünün. En küçük kareler yöntemine göre sapmaların minimum kareleri toplamı için koşul şu şekilde yazılır: Tablonun düğüm noktalarının koordinatları; Doğrusal bir ilişki olarak belirtilen yaklaşık işlevin bilinmeyen katsayıları. Bir fonksiyonun minimumunun varlığı için gerekli koşul, bilinmeyen değişkenlere göre kısmi türevlerinin sıfıra eşit olmasıdır. Sonuç olarak, aşağıdaki denklem sistemini elde ederiz:
Ortaya çıkan lineer denklem sistemini dönüştürelim.
Elde edilen lineer denklem sistemini çözüyoruz. Analitik formda yaklaşıklık fonksiyonunun katsayıları aşağıdaki gibi belirlenir (Cramer'ın yöntemi):
Bu katsayılar, verilen tablo değerlerinden (deneysel veriler) yaklaşma fonksiyonunun karelerinin toplamını en aza indirme kriterine göre doğrusal bir yaklaşım fonksiyonunun oluşturulmasını sağlar. En küçük kareler yöntemini uygulamak için algoritma 1. İlk veriler: N ölçüm sayısı ile bir dizi deneysel veri verildi Yaklaşan polinomun derecesi (m) verilir 2. Hesaplama algoritması: 2.1. Boyutlu bir denklem sistemi oluşturmak için katsayılar belirlenir.
Denklem sisteminin katsayıları (denklemin sol tarafı)
Lineer denklem sisteminin serbest üyeleri (denklemin sağ tarafı)
2.2. Boyutlu bir lineer denklem sisteminin oluşumu.
2.3. m dereceli yaklaşık polinomun bilinmeyen katsayılarını belirlemek için bir lineer denklem sisteminin çözümü. 2.4 Yaklaşık polinomun tüm düğüm noktalarındaki ilk değerlerden kare sapmalarının toplamının belirlenmesi
Sapmaların karelerinin toplamının bulunan değeri, mümkün olan en düşük değerdir. Diğer Fonksiyonlarla Yaklaşım En küçük kareler yöntemine göre ilk verileri yaklaştırırken, bazen yaklaşık bir fonksiyon olarak bir logaritmik fonksiyon, bir üstel fonksiyon ve bir güç fonksiyonunun kullanıldığına dikkat edilmelidir. Günlük yaklaşımı Yaklaşım fonksiyonunun, formun logaritmik bir fonksiyonu tarafından verildiği durumu düşünün: | ||