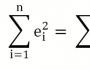Katseandmete lähendamine. Vähima ruudu meetod. Funktsiooni lähendamine vähimruutude meetodil Kasutades lähendamiseks vähimruutude meetodit
Pärast joondamist saame funktsiooni järgmisel kujul: g (x) = x + 1 3 + 1 .
Saame neid andmeid lähendada lineaarse seosega y = a x + b, arvutades vastavad parameetrid. Selleks peame rakendama niinimetatud vähimruutude meetodit. Samuti peate tegema joonise, et kontrollida, milline joon joondab katseandmeid kõige paremini.
Mis täpselt on OLS (vähimruutude meetod)
Peamine asi, mida peame tegema, on leida sellised lineaarsed sõltuvuskoefitsiendid, mille puhul kahe muutuja funktsiooni väärtus F (a, b) = ∑ i = 1 n (yi - (axi + b)) 2 on väikseim . Teisisõnu, teatud a ja b väärtuste korral on esitatud andmete ruudus hälbete summa saadud sirgest minimaalne. See on vähimruutude meetodi tähendus. Näite lahendamiseks peame vaid leidma kahe muutuja funktsiooni ekstreemumi.
Kuidas tuletada koefitsientide arvutamise valemeid
Koefitsientide arvutamise valemite tuletamiseks on vaja koostada ja lahendada kahe muutujaga võrrandisüsteem. Selleks arvutame avaldise F (a , b) = ∑ i = 1 n (y i - (a x i + b)) 2 osatuletised a ja b suhtes ning võrdsustame need 0-ga.
δ F (a , b) δ a = 0 δ F (a , b) δ b = 0 ⇔ - 2 ∑ i = 1 n (yi - (axi + b)) xi = 0 - 2 ∑ i = 1 n ( yi - (axi + b)) = 0 ⇔ a ∑ i = 1 nxi 2 + b ∑ i = 1 nxi = ∑ i = 1 nxiyia ∑ i = 1 nxi + ∑ i = 1 nb = ∑ i = 1 a nb = ∑ i = 1 ∑ i = 1 nxi 2 + b ∑ i = 1 nxi = ∑ i = 1 nxiyia ∑ i = 1 nxi + nb = ∑ i = 1 nyi
Võrrandisüsteemi lahendamiseks võite kasutada mis tahes meetodeid, näiteks asendus- või Crameri meetodit. Selle tulemusena peaksime saama valemid, mis arvutavad koefitsiendid vähimruutude meetodil.
n ∑ i = 1 n x i y i - ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n - ∑ i = 1 n x i 2 b = ∑ i = 1 a n 1 n i
Oleme välja arvutanud muutujate väärtused, mille jaoks funktsioon on
F (a , b) = ∑ i = 1 n (y i - (a x i + b)) 2 võtab minimaalse väärtuse. Kolmandas lõigus tõestame, miks see nii on.
See on vähimruutude meetodi rakendamine praktikas. Tema valem, mida kasutatakse parameetri a leidmiseks, sisaldab ∑ i = 1 n x i, ∑ i = 1 n y i, ∑ i = 1 n x i y i, ∑ i = 1 n x i 2 ja parameetrit
n - see tähistab katseandmete hulka. Soovitame teil arvutada iga summa eraldi. Koefitsiendi väärtus b arvutatakse kohe pärast a .
Tuleme tagasi algse näite juurde.
Näide 1
Siin on meil n võrdne viiega. Koefitsientide valemitesse kuuluvate nõutavate summade arvutamise mugavamaks muutmiseks täidame tabeli.
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | ∑ i = 1 5 | |
| x i | 0 | 1 | 2 | 4 | 5 | 12 |
| y i | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 | 12 , 9 |
| x i y i | 0 | 2 , 4 | 5 , 2 | 11 , 2 | 15 | 33 , 8 |
| x i 2 | 0 | 1 | 4 | 16 | 25 | 46 |
Lahendus
Neljas rida sisaldab andmeid, mis on saadud teise rea väärtuste korrutamisel kolmanda väärtustega iga üksikisiku i kohta. Viies rida sisaldab teise ruudu andmeid. Viimane veerg näitab üksikute ridade väärtuste summasid.
Kasutame vajalike koefitsientide a ja b arvutamiseks vähimruutude meetodit. Selleks asendage soovitud väärtused viimasest veerust ja arvutage summad:
n ∑ i = 1 nxiyi - ∑ i = 1 nxi ∑ i = 1 nyin ∑ i = 1 n - ∑ i = 1 nxi 2 b = ∑ i = 1 nyi - a ∑ i = 1 nxin, ∑ i = 1 nxin, 33 = 5 ⇒ 3 - 12 12, 9 5 46 - 12 2 b = 12, 9 - a 12 5 ⇒ a ≈ 0, 165 b ≈ 2, 184
Saime, et soovitud ligikaudne sirge näeb välja selline y = 0, 165 x + 2, 184. Nüüd peame kindlaks määrama, milline rida on andmetele kõige paremini ligikaudne - g (x) = x + 1 3 + 1 või 0, 165 x + 2, 184. Teeme hinnangu vähimruutude meetodil.
Vea arvutamiseks peame leidma joontelt σ 1 = ∑ i = 1 n (yi - (axi + bi)) 2 ja σ 2 = ∑ i = 1 n (yi -) andmete ruuduhälbete summad. g (xi)) 2, vastab miinimumväärtus sobivamale reale.
σ 1 = ∑ i = 1 n (yi - (axi + bi)) 2 = = ∑ i = 1 5 (yi - (0, 165 xi + 2, 184)) 2 ≈ 0, 019 σ 2 = ∑ i = 1 n (yi - g (xi)) 2 = = ∑ i = 1 5 (yi - (xi + 1 3 + 1)) 2 ≈ 0, 096
Vastus: alates σ 1< σ 2 , то прямой, наилучшим образом аппроксимирующей исходные данные, будет
y = 0, 165 x + 2, 184.
Vähimruutude meetod on graafilisel joonisel selgelt näidatud. Punane joon tähistab sirget g (x) = x + 1 3 + 1, sinine joon tähistab y = 0, 165 x + 2, 184. Algandmed on tähistatud roosade täppidega.
Selgitame, miks on vaja täpselt seda tüüpi lähendusi.
Neid saab kasutada nii andmete silumist nõudvates probleemides kui ka nendes, kus andmeid on vaja interpoleerida või ekstrapoleerida. Näiteks eespool käsitletud ülesandes võiks leida vaadeldava suuruse y väärtuse x = 3 või x = 6 juures. Oleme sellistele näidetele pühendanud eraldi artikli.
LSM meetodi tõestus
Et funktsioon saaks arvutatud a ja b jaoks minimaalse väärtuse, on vajalik, et antud punktis vormi F (a, b) funktsiooni diferentsiaali ruutkuju maatriks = ∑ i = 1 n ( yi - (axi + b)) 2 olema positiivne kindel. Näitame teile, kuidas see peaks välja nägema.
Näide 2
Meil on teise järgu diferentsiaal järgmisel kujul:
d 2 F (a ; b) = δ 2 F (a ; b) δ a 2 d 2 a + 2 δ 2 F (a ; b) δ a δ bdadb + δ 2 F (a ; b) δ b 2 d 2b
Lahendus
δ 2 F (a ; b) δ a 2 = δ δ F (a ; b) δ a δ a = = δ - 2 ∑ i = 1 n (yi - (axi + b)) xi δ a = 2 ∑ i = 1 n (xi) 2 δ 2 F (a ; b) δ a δ b = δ δ F (a ; b) δ a δ b = = δ - 2 ∑ i = 1 n (yi - (axi + b) ) xi δ b = 2 ∑ i = 1 nxi δ 2 F (a ; b) δ b 2 = δ δ F (a ; b) δ b δ b = δ - 2 ∑ i = 1 n (yi - (axi + b)) δ b = 2 ∑ i = 1 n (1) = 2 n
Teisisõnu saab selle kirjutada järgmiselt: d 2 F (a ; b) = 2 ∑ i = 1 n (x i) 2 d 2 a + 2 2 ∑ x i i = 1 n d a d b + (2 n) d 2 b .
Oleme saanud ruutkujulise maatriksi M = 2 ∑ i = 1 n (x i) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n .
Sel juhul ei muutu üksikute elementide väärtused sõltuvalt a-st ja b-st. Kas see maatriks on positiivne? Sellele küsimusele vastamiseks kontrollime, kas selle nurgelised alaealised on positiivsed.
Arvutage esimest järku nurk-moll: 2 ∑ i = 1 n (x i) 2 > 0 . Kuna punktid x i ei lange kokku, on ebavõrdsus range. Peame seda edasistes arvutustes meeles.
Arvutame teist järku nurk-molli:
d e t (M) = 2 ∑ i = 1 n (x i) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n = 4 n ∑ i = 1 n (x i) 2 - 12 n i = i
Seejärel jätkame matemaatilist induktsiooni kasutades ebavõrdsuse n ∑ i = 1 n (x i) 2 - ∑ i = 1 n x i 2 > 0 tõestamist.
- Kontrollime, kas see võrratus kehtib suvalise n korral. Võtame 2 ja arvutame:
2 ∑ i = 1 2 (xi) 2 - ∑ i = 1 2 xi 2 = 2 x 1 2 + x 2 2 - x 1 + x 2 2 = = x 1 2 - 2 x 1 x 2 + x 2 2 = x 1 + x 2 2 > 0
Saime õige võrdsuse (kui väärtused x 1 ja x 2 ei ühti).
- Oletame, et see ebavõrdsus kehtib n korral, s.o. n ∑ i = 1 n (x i) 2 - ∑ i = 1 n x i 2 > 0 – tõene.
- Nüüd tõestame n + 1 kehtivust, s.o. et (n + 1) ∑ i = 1 n + 1 (xi) 2 - ∑ i = 1 n + 1 xi 2 > 0, kui n ∑ i = 1 n (xi) 2 - ∑ i = 1 nxi 2 > 0 .
Arvutame:
(n + 1) ∑ i = 1 n + 1 (xi) 2 - ∑ i = 1 n + 1 xi 2 = = (n + 1) ∑ i = 1 n (xi) 2 + xn + 1 2 - ∑ i = 1 nxi + xn + 1 2 = = n ∑ i = 1 n (xi) 2 + n xn + 1 2 + ∑ i = 1 n (xi) 2 + xn + 1 2 - - ∑ i = 1 nxi 2 + 2 xn + 1 ∑ i = 1 nxi + xn + 1 2 = = ∑ i = 1 n (xi) 2 - ∑ i = 1 nxi 2 + n xn + 1 2 - xn + 1 ∑ i = 1 nxi + ∑ i = 1 n (xi) 2 = = ∑ i = 1 n (xi) 2 - ∑ i = 1 nxi 2 + xn + 1 2 - 2 xn + 1 x 1 + x 1 2 + + xn + 1 2 - 2 xn + 1 x 2 + x 2 2 + . . . + xn + 1 2 - 2 xn + 1 x 1 + xn 2 = = n ∑ i = 1 n (xi) 2 - ∑ i = 1 nxi 2 + + (xn + 1 - x 1) 2 + (xn + 1) - x 2) 2 + . . . + (x n - 1 - x n) 2 > 0
Sulgudes sisalduv avaldis on suurem kui 0 (alusel, mida me 2. sammus eeldasime), ja ülejäänud terminid on suuremad kui 0, kuna need on kõik arvude ruudud. Oleme ebavõrdsust tõestanud.
Vastus: leitud a ja b vastavad funktsiooni F (a, b) = ∑ i = 1 n (yi - (axi + b)) 2 väikseimale väärtusele, mis tähendab, et need on vähimruutude meetodi soovitud parameetrid (LSM).
Kui märkate tekstis viga, tõstke see esile ja vajutage Ctrl+Enter
Sellel on palju rakendusi, kuna see võimaldab antud funktsiooni ligikaudselt esitada teiste lihtsamate funktsioonidega. LSM võib olla väga kasulik vaatluste töötlemisel ja seda kasutatakse aktiivselt mõne koguse hindamiseks teiste juhuslikke vigu sisaldavate mõõtmistulemuste põhjal. Sellest artiklist saate teada, kuidas Excelis vähimruutude arvutusi rakendada.
Probleemi avaldus konkreetsel näitel
Oletame, et on kaks indikaatorit X ja Y. Veelgi enam, Y sõltub X-st. Kuna OLS pakub meile huvi regressioonanalüüsi seisukohalt (Excelis on selle meetodid realiseeritud sisseehitatud funktsioonide abil), tuleks kohe edasi minna. konkreetse probleemi käsitlemiseks.
Olgu siis X toidupoe müügipind ruutmeetrites ja Y aastakäive miljonites rublades.
Nõutav on teha prognoos, milline on kaupluse käive (Y), kui sellel on üks või teine müügipind. Ilmselgelt funktsioon Y = f (X) kasvab, kuna hüpermarket müüb rohkem kaupa kui müügilett.
Paar sõna ennustuseks kasutatud algandmete õigsusest
Oletame, et meil on n poe andmetest koostatud tabel.
Matemaatilise statistika järgi on tulemused enam-vähem õiged, kui uurida vähemalt 5-6 objekti andmeid. Samuti ei saa kasutada "anomaaalseid" tulemusi. Eelkõige võib elitaarse väikese butiigi käive olla mitu korda suurem kui "masmarketi" klassi suurte kaupluste käive.
Meetodi olemus
Tabeli andmeid saab kuvada Descartes'i tasapinnal punktidena M 1 (x 1, y 1), ... M n (x n, y n). Nüüd taandatakse ülesande lahendus lähendava funktsiooni y = f (x) valikule, mille graafik läbib võimalikult lähedalt punktidele M 1, M 2, .. M n .
Muidugi võite kasutada kõrgetasemelist polünoomi, kuid seda valikut pole mitte ainult raske rakendada, vaid see on lihtsalt vale, kuna see ei kajasta peamist suundumust, mida tuleb tuvastada. Kõige mõistlikum lahendus on leida sirge y = ax + b, mis kõige paremini lähendab katseandmeid või õigemini koefitsiente - a ja b.
Täpsusskoor
Mis tahes lähendamise puhul on selle täpsuse hindamine eriti oluline. Tähistage e i-ga punkti x i funktsionaalsete ja eksperimentaalsete väärtuste erinevus (hälve), st e i = y i - f (x i).
Ilmselt võite lähenduse täpsuse hindamiseks kasutada hälvete summat, st kui valite sirge X-i sõltuvuse Y-st ligikaudseks esitamiseks, tuleks eelistada seda, millel on väikseim väärtus. summast ei kõigis vaadeldavates punktides. Kõik pole aga nii lihtne, sest koos positiivsete kõrvalekalletega on praktiliselt olemas ka negatiivsed.
Probleemi saate lahendada kõrvalekallete moodulite või nende ruutude abil. Viimane meetod on kõige laialdasemalt kasutatav. Seda kasutatakse paljudes valdkondades, sealhulgas regressioonanalüüsis (Excelis viiakse selle rakendamine läbi kahe sisseehitatud funktsiooni abil) ja selle tõhusus on juba ammu tõestatud.
Vähima ruudu meetod
Nagu teate, on Excelis sisseehitatud automaatse summa funktsioon, mis võimaldab teil arvutada kõigi valitud vahemikus asuvate väärtuste väärtused. Seega ei takista miski meil avaldise väärtust (e 1 2 + e 2 2 + e 3 2 + ... e n 2) arvutamast.
Matemaatilises tähistuses näeb see välja järgmine:

Kuna algselt otsustati ligikaudselt sirgjoont kasutada, on meil:

Seega, ülesanne leida sirgjoon, mis kõige paremini kirjeldab konkreetset seost X ja Y vahel, võrdub kahe muutuja funktsiooni miinimumi arvutamisega:

Selleks tuleb uute muutujate a ja b osas võrdsustada osatuletistega null ning lahendada primitiivne süsteem, mis koosneb kahest võrrandist kahe tundmatu kujuga:

Pärast lihtsaid teisendusi, sealhulgas 2-ga jagamist ja summadega manipuleerimist, saame:

Lahendades seda näiteks Crameri meetodil, saame kindlate koefitsientidega a * ja b * statsionaarse punkti. See on miinimum, st et ennustada, milline on kaupluse käive teatud piirkonnas, sobib sirge y = a * x + b *, mis on vaadeldava näite regressioonimudel. Muidugi ei võimalda see teil täpset tulemust leida, kuid aitab saada aimu, kas konkreetse piirkonna jaoks poe ostmine laenuga tasub end ära.
Kuidas rakendada Excelis vähimruutude meetodit
Excelis on funktsioon vähimruutude väärtuse arvutamiseks. Sellel on järgmine vorm: TREND (teadaolevad Y väärtused; teadaolevad X väärtused; uued X väärtused; konstant). Rakendame oma tabelisse OLS-i arvutamise valemit Excelis.
Selleks sisestage lahtrisse, kus peaks olema Exceli vähimruutude meetodil arvutamise tulemus, märk “=” ja valige funktsioon “TREND”. Avanevas aknas täitke vastavad väljad, tõstes esile:
- Y teadaolevate väärtuste vahemik (antud juhul andmed käibe kohta);
- vahemik x 1 , …x n , st kaubanduspinna suurus;
- ja x teadaolevad ja tundmatud väärtused, mille jaoks peate välja selgitama käibe suuruse (teavet nende asukoha kohta töölehel vt allpool).
Lisaks on valemis loogiline muutuja "Const". Kui sisestate sellele vastavale väljale 1, tähendab see, et arvutused tuleks läbi viia, eeldades, et b \u003d 0.
Kui teil on vaja teada prognoosi rohkem kui ühe x väärtuse jaoks, siis pärast valemi sisestamist ei tohiks vajutada "Enter", vaid peate sisestama kombinatsiooni "Shift" + "Control" + "Enter" ("Sisesta" ) klaviatuuril.
Mõned funktsioonid
Regressioonanalüüs on kättesaadav isegi mannekeenidele. Tundmatute muutujate massiivi väärtuse ennustamiseks mõeldud Exceli valemit - "TREND" - saavad kasutada isegi need, kes pole vähimruutude meetodist kuulnudki. Piisab lihtsalt selle töö mõne funktsiooni tundmisest. Eriti:
- Kui korraldate muutuja y teadaolevate väärtuste vahemiku ühte ritta või veergu, siis tajub programm iga teadaolevate väärtustega x rida (veerg) eraldi muutujana.
- Kui teadaoleva x-ga vahemikku TREND aknas pole määratud, siis Excelis funktsiooni kasutamise korral käsitleb programm seda täisarvudest koosneva massiivina, mille arv vastab antud väärtustega vahemikule muutujast y.
- "Prognoositud" väärtuste massiivi väljastamiseks tuleb trendi avaldis sisestada massiivivalemina.
- Kui uusi x väärtusi pole määratud, loeb funktsioon TREND need võrdseks teadaolevatega. Kui neid ei täpsustata, võetakse argumendiks massiiv 1; 2; 3; 4;…, mis on proportsionaalne juba antud parameetritega y vahemikuga.
- Uusi x väärtusi sisaldav vahemik peab sisaldama sama või enamat rida või veergu kui antud y väärtustega vahemik. Teisisõnu peab see olema proportsionaalne sõltumatute muutujatega.
- Teadaolevate x väärtustega massiiv võib sisaldada mitut muutujat. Kui aga räägime ainult ühest, siis on nõutav, et antud x ja y väärtustega vahemikud oleksid proportsionaalsed. Mitme muutuja puhul on vajalik, et antud y väärtustega vahemik mahuks ühte veergu või ühte ritta.

PROGNOOS funktsioon
Seda rakendatakse mitme funktsiooni abil. Üks neist kannab nime "ENNUSTUS". See on sarnane TRENDiga, st annab vähimruutude meetodil tehtud arvutuste tulemuse. Kuid ainult ühe X puhul, mille Y väärtus on teadmata.
Nüüd teate mannekeenide Exceli valemeid, mis võimaldavad ennustada indikaatori tulevase väärtuse väärtust lineaarse trendi järgi.
3. Funktsioonide lähendamine meetodi abil
vähimruudud
Katse tulemuste töötlemisel kasutatakse vähimruutude meetodit ligikaudsed (ligikaudsed hinnangud) eksperimentaalsed andmed analüütiline valem. Valemi konkreetne vorm valitakse reeglina füüsilistest kaalutlustest lähtuvalt. Need valemid võivad olla:
![]()
![]()
ja teised.
Vähimruutude meetodi olemus on järgmine. Mõõtmistulemused esitatakse tabelis:
|
laud 4 |
||||
|
x n |
||||
|
y n |
||||
|
(3.1) |
kus f on tuntud funktsioon, a 0, a 1, …, a m - tundmatud konstantsed parameetrid, mille väärtused tuleb leida. Vähimruutude meetodi puhul peetakse funktsiooni (3.1) lähendamist eksperimentaalsele sõltuvusele parimaks, kui tingimus
|
(3.2) |
st summad a soovitud analüütilise funktsiooni ruudus kõrvalekalded eksperimentaalsest sõltuvusest peaksid olema minimaalsed .
Pange tähele, et funktsioon K helistas inviscid.

Alates lahknevusest

siis on sellel miinimum. Mitme muutuja funktsiooni miinimumi vajalik tingimus on selle funktsiooni kõigi osatuletiste võrdsus parameetrite suhtes nulliga. Seega leitakse ligikaudse funktsiooni (3.1) parameetrite parimad väärtused, st need väärtused, mille jaoks Q = Q (a 0, a 1, …, a m ) on minimaalne, taandub võrrandisüsteemi lahendamiseks:
|
(3.3) |
Vähimruutude meetodile saab anda järgmise geomeetrilise tõlgenduse: antud tüüpi joonte lõpmatu perekonna hulgast leitakse üks sirge, mille korral saadakse katsepunktide ordinaatide ja punktide vastavate ordinaatide ruudu erinevuste summa. selle sirge võrrandiga leitud on väikseim.
Lineaarfunktsiooni parameetrite leidmine
Olgu katseandmed esindatud lineaarse funktsiooniga:
Sellised väärtused tuleb valida a ja b , mille jaoks funktsioon
|
(3.4) |
saab olema minimaalne. Funktsiooni (3.4) miinimumi vajalikud tingimused taandatakse võrrandisüsteemiks:
|
|
Pärast teisendusi saame kahe tundmatuga lineaarvõrrandi süsteemi:
|
|
(3.5) |
mille lahendamisel leiame parameetrite soovitud väärtused a ja b.
Ruutfunktsiooni parameetrite leidmine
Kui lähendavaks funktsiooniks on ruutsõltuvus
siis selle parameetrid a , b , c leidke funktsiooni miinimumtingimusest:
|
(3.6) |
Funktsiooni (3.6) miinimumtingimused taandatakse võrrandisüsteemiks:
|
|
Pärast teisendusi saame kolme tundmatuga lineaarvõrrandi süsteemi:
|
|
(3.7) |
juures mille lahendamisel leiame parameetrite soovitud väärtused a , b ja c .
Näide . Eksperimendi tulemusena saadakse järgmine väärtuste tabel x ja y:
|
laud 5 |
||||||||
|
y i |
0,705 |
0,495 |
0,426 |
0,357 |
0,368 |
0,406 |
0,549 |
0,768 |
Katseandmeid on vaja ligikaudselt lineaarsete ja ruutfunktsioonide abil.
Lahendus. Lähendavate funktsioonide parameetrite leidmine taandub lineaarvõrrandisüsteemide (3.5) ja (3.7) lahendamisele. Probleemi lahendamiseks kasutame arvutustabeliprotsessorit excel.
1. Esmalt ühendame lehed 1 ja 2. Sisestage katseväärtused x i ja y i veergudeks A ja B, alustades teisest reast (esimesele reale paneme veergude pealkirjad). Seejärel arvutame nende veergude summad ja paneme need kümnendasse ritta.
Veergudes C–G asetage vastavalt arvutus ja liitmine
2. Haakige lehed lahti. Täiendavad arvutused tehakse sarnasel viisil lineaarse sõltuvuse jaoks lehelt 1 ja ruutsõltuvuse jaoks lehelt 2.
3. Saadud tabeli alla moodustame koefitsientide maatriksi ja vabade liikmete veeruvektori. Lahendame lineaarvõrrandisüsteemi järgmise algoritmi järgi:
Pöördmaatriksi arvutamiseks ja maatriksite korrutamiseks kasutame Meister funktsioonid ja funktsioonid MOBR Ja MUMNOŽH.
4. Lahtriplokis H2: H 9 saadud koefitsientide põhjal arvutame ligikaudsed väärtused polünoomy i arvut., plokis I 2: I 9 - kõrvalekalded D y i = y i eksp. - y i arvut., veerus J – lahknevus:
Tabelid saadud ja ehitatud kasutades Diagrammide võlurid graafikud on näidatud joonistel 6, 7, 8.

Riis. 6. Lineaarfunktsiooni koefitsientide arvutamise tabel,
ligikaudne eksperimentaalsed andmed.

Riis. 7. Ruutfunktsiooni kordajate arvutamise tabel,
ligikaudneeksperimentaalsed andmed.

Riis. 8. Lähenduse tulemuste graafiline esitus
eksperimentaalandmete lineaar- ja ruutfunktsioonid.
Vastus. Eksperimentaalsed andmed lähendati lineaarse sõltuvuse alusel y = 0,07881 x + 0,442262 jääkidega K = 0,165167 ja ruutsõltuvus y = 3,115476 x 2 – 5,2175 x + 2,529631 jääkidega K = 0,002103 .
Ülesanded. Lähendage tabel-, lineaar- ja ruutfunktsioonidega antud funktsiooni.
|
Tabel 6 |
|||||||||
|
№0 |
x |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
|
y |
3,030 |
3,142 |
3,358 |
3,463 |
3,772 |
3,251 |
3,170 |
3,665 |
|
|
№ 1 |
|||||||||
|
3,314 |
3,278 |
3,262 |
3,292 |
3,332 |
3,397 |
3,487 |
3,563 |
||
|
№ 2 |
|||||||||
|
1,045 |
1,162 |
1,264 |
1,172 |
1,070 |
0,898 |
0,656 |
0,344 |
||
|
№ 3 |
|||||||||
|
6,715 |
6,735 |
6,750 |
6,741 |
6,645 |
6,639 |
6,647 |
6,612 |
||
|
№ 4 |
|||||||||
|
2,325 |
2,515 |
2,638 |
2,700 |
2,696 |
2,626 |
2,491 |
2,291 |
||
|
№ 5 |
|||||||||
|
1.752 |
1,762 |
1,777 |
1,797 |
1,821 |
1,850 |
1,884 |
1,944 |
||
|
№ 6 |
|||||||||
|
1,924 |
1,710 |
1,525 |
1,370 |
1,264 |
1,190 |
1,148 |
1,127 |
||
|
№ 7 |
|||||||||
|
1,025 |
1,144 |
1,336 |
1,419 |
1,479 |
1,530 |
1,568 |
1,248 |
||
|
№ 8 |
|||||||||
|
5,785 |
5,685 |
5,605 |
5,545 |
5,505 |
5,480 |
5,495 |
5,510 |
||
|
№ 9 |
|||||||||
|
4,052 |
4,092 |
4,152 |
4,234 |
4,338 |
4,468 |
4,599 |
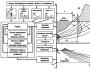
KURSUSETÖÖ Funktsiooni lähendamine vähimruutude meetodil Sissejuhatus empiiriline mathcad lähendus Kursusetöö eesmärk on süvendada informaatikaalaseid teadmisi, arendada ja kinnistada oskusi töötamiseks tabelarvutusprotsessoriga Microsoft Excel ja MathCAD. Nende rakendus arvuti abil ülesannete lahendamiseks uurimistööga seotud ainevaldkonnast. Igas ülesandes on sõnastatud ülesande tingimused, lähteandmed, tulemuste väljastamise vorm, välja toodud peamised matemaatilised sõltuvused ülesande lahendamiseks Kontrollarvutus võimaldab kontrollida programmi korrektset toimimist. Lähenduse mõiste on mõnede matemaatiliste objektide (näiteks arvud või funktsioonid) ligikaudne väljendus teiste lihtsamate, mugavamate kasutada või lihtsalt paremini tuntud objektide kaudu. Teadusuuringutes kasutatakse lähendamist empiiriliste tulemuste kirjeldamiseks, analüüsimiseks, üldistamiseks ja edasiseks kasutamiseks. Teatavasti võib väärtuste vahel olla täpne (funktsionaalne) seos, kui argumendi üks väärtus vastab ühele konkreetsele väärtusele, ja vähemtäpne (korrelatsioon) seos, kui argumendi üks konkreetne väärtus vastab ligikaudsele väärtusele. või mõni funktsiooniväärtuste komplekt, mis on üksteisele enam-vähem lähedased. Teadusliku uurimistöö tegemisel, vaatluse või katse tulemuste töötlemisel tuleb enamasti tegeleda teise variandiga. Erinevate näitajate kvantitatiivsete sõltuvuste uurimisel, mille väärtused määratakse empiiriliselt, on reeglina mõningane varieeruvus. Osaliselt määrab selle uuritud elutu ja eriti eluslooduse objektide heterogeensus, osalt vaatluse ja materjalide kvantitatiivse töötlemise viga. Viimast komponenti ei ole alati võimalik täielikult kõrvaldada, seda saab minimeerida ainult sobiva uurimismeetodi hoolika valiku ja töö täpsusega. Tehnoloogiliste protsesside ja tootmiste automatiseerimise valdkonna spetsialistid tegelevad suure hulga katseandmetega, mille töötlemiseks kasutatakse arvutit. Arvutuste lähteandmeid ja saadud tulemusi saab esitada tabelina, kasutades tabeliprotsessoreid (tabeleid) ja eelkõige Excelit. Arvutiteaduse kursusetöö võimaldab kinnistada ja arendada oskusi töötada põhiliste arvutitehnoloogiate abil kutsetegevuse valdkonna ülesannete lahendamisel - arvutialgebrasüsteem arvutipõhise projekteerimise süsteemide klassist, mis on keskendunud ettevalmistamisele arvutuste ja visuaalse toega interaktiivseid dokumente, on lihtne kasutada ja meeskonnatööks taotleda. 1. Üldine informatsioon Väga sageli, eriti empiiriliste andmete analüüsimisel, on vaja selgesõnaliselt leida suuruste funktsionaalne seos xJa juures, mis saadakse mõõtmiste tulemusena. Kahe suuruse x ja y vahelise seose analüütilises uuringus tehakse rida vaatlusi ja tulemuseks on väärtuste tabel: xx1 x1 xiXnyy1 y1 yiYn See tabel saadakse tavaliselt mõne katse tulemusena, mille käigus x,(sõltumatu väärtuse) määrab katse läbiviija ja y,saadud kogemuse tulemusena. Seetõttu need väärtused y,nimetatakse empiirilisteks või eksperimentaalseteks väärtusteks. Väärtuste x ja y vahel on funktsionaalne seos, kuid selle analüütiline vorm on tavaliselt teadmata, seega tekib praktiliselt oluline ülesanne - leida empiiriline valem y=f (x; a 1, a 2,…, olen ), (1) (kus a1 , a2 ,…, am- parameetrid), mille väärtused on x=x,ilmselt erineks katseväärtustest vähe y, (i = 1,2,…, P). Tavaliselt märkige funktsioonide klass (näiteks lineaarne, võimsus, eksponentsiaalne jne), mille hulgast funktsioon on valitud f(x)ja seejärel määratakse parameetrite parimad väärtused. Kui empiirilises valemis (1) asendame initsiaaliga x,siis saame teoreetilised väärtused YTi= f (xi; a 1, a 2……am) , kus i = 1,2,…, n. Erinevused yiT- kelli, nimetatakse hälveteks ja need tähistavad vertikaalseid kaugusi punktidest Miempiirilise funktsiooni graafikule. Vähimruutude meetodi järgi parimad koefitsiendid a1 , a2 ,…, amarvestatakse neid, mille puhul on leitud empiirilise funktsiooni ruudus hälvete summa funktsiooni antud väärtustest saab olema minimaalne. Selgitame vähimruutude meetodi geomeetrilist tähendust. Iga numbripaar ( xi, yi) lähtetabelist määratleb punkti Mipinnal XOY.Valemi (1) kasutamine koefitsientide erinevate väärtuste jaoks a1 , a2 ,…, amon võimalik koostada rida kõveraid, mis on funktsiooni (1) graafikud. Probleemiks on koefitsientide määramine a1 , a2 ,…, amnii et vertikaalsete kauguste ruutude summa punktidest Mi (xi, yi) funktsiooni (1) graafikule oli väikseim (joonis 1). Empiirilise valemi koostamine koosneb kahest etapist: selle valemi üldkuju väljaselgitamine ja selle parimate parameetrite määramine. Kui antud suuruste x ja vahelise seose olemus y, siis on empiirilise sõltuvuse vorm meelevaldne. Eelistatakse lihtsaid, hea täpsusega valemeid. Empiirilise valemi edukas valik sõltub suuresti uurija teadmistest ainevaldkonnas, mille abil saab ta teoreetilistest kaalutlustest funktsioonide klassi näidata. Suur tähtsus on saadud andmete esitamisel Descartes'i või spetsiaalsetes koordinaatsüsteemides (poollogaritmiline, logaritmiline jne). Punktide asukoha järgi võib ligikaudselt oletada sõltuvuse üldist vormi, tuvastades sarnasuse konstrueeritud graafiku ja tuntud kõverate näidiste vahel. Parimate koefitsientide kindlaksmääramine a1 , a2,…, amsisaldub tuntud analüütiliste meetoditega koostatud empiirilises valemis. Koefitsientide hulga leidmiseks a1 , a2 ……am, mis annavad valemiga (2) defineeritud funktsiooni S miinimumi, kasutame mitme muutuja funktsiooni ekstreemumi jaoks vajalikku tingimust - osatuletisi võrdsust nulliga. Selle tulemusena saame koefitsientide määramiseks normaalse süsteemi ai(i = 1,2,…, m): Seega koefitsientide leidmine aitaandub lahendussüsteemiks (3). See süsteem on lihtsustatud, kui empiiriline valem (1) on parameetrite suhtes lineaarne ai, siis süsteem (3) on lineaarne. 1.1 Lineaarne seos Süsteemi (3) konkreetne vorm sõltub empiiriliste valemite klassist, millest me otsime sõltuvust (1). Lineaarse seose korral y=a1 + a2 xsüsteem (3) on järgmisel kujul: Seda lineaarset süsteemi saab lahendada mis tahes tuntud meetodiga (Gaussi meetod, lihtsad iteratsioonid, Crameri valemid). 1.2 Ruutsõltuvus Ruutsõltuvuse korral y=a1 + a2 x + a3x 2süsteem (3) on järgmisel kujul: 1.3 Eksponentsõltuvus Mõnel juhul võetakse empiirilise valemina funktsioon, millesse mittelineaarselt sisenevad ebakindlad koefitsiendid. Sellisel juhul võib mõnikord probleemi lineariseerida, st. taandada lineaarseks. Selliste sõltuvuste hulgas on eksponentsiaalne sõltuvus y=a1 * ea2x (6) kus a 1Ja a 2, määratlemata koefitsiendid. Lineariseerimine saavutatakse võrdsuse (6) logaritmi võtmisega, mille järel saame seose ln y = ln a 1+a 2x (7) Tähistage ln juuresja ln axvastavalt läbi tJa c, siis sõltuvuse (6) saab kirjutada kujul t = a1 + a2 X, mis võimaldab meil koos asendusega rakendada valemeid (4). a1 peal cJa juuresi peal ti 1.4 Korrelatsiooniteooria elemendid Taastatud funktsionaalse sõltuvuse graafik y(x)vastavalt mõõtmistulemustele (x i, juuresi),i = 1,2, K, nnimetatakse regressioonikõveraks. Konstrueeritud regressioonikõvera ja katse tulemustega vastavuse kontrollimiseks võetakse tavaliselt kasutusele järgmised arvulised karakteristikud: korrelatsioonikordaja (lineaarne sõltuvus), korrelatsioonikordaja ja determinismikordaja. Sel juhul on tulemused tavaliselt rühmitatud ja esitatud korrelatsioonitabeli kujul. Selle tabeli igas lahtris on toodud numbrid niJ - need paarid (x, y), mille komponendid jäävad iga muutuja vastavate rühmitusvahemike sisse. Eeldades, et rühmitamisintervallide pikkused (iga muutuja jaoks) on üksteisega võrdsed, vali keskpunktid x i(vastavalt juuresi) nendest intervallidest ja arvust niJ- arvutuste aluseks. Korrelatsioonikordaja on sõltuvate juhuslike muutujate vahelise lineaarse seose mõõt: see näitab, kui hästi saab keskmiselt ühte muutujatest teise lineaarse funktsioonina esitada. Korrelatsioonikordaja arvutatakse järgmise valemiga: kus ja on vastavalt aritmeetiline keskmine X Ja juures. Korrelatsioonikordaja juhuslike suuruste vahel ei ületa absoluutväärtuses 1. Mida lähemal on |р| 1-ni, seda tihedam on lineaarne seos x ja vahel y. Mittelineaarse korrelatsiooni korral paiknevad tingimuslikud keskmised kõverjoone lähedal. Sel juhul on soovitatav kasutada seose tugevuse tunnusena korrelatsioonisuhet, mille tõlgendamine ei sõltu uuritava sõltuvuse tüübist. Korrelatsioonisuhe arvutatakse järgmise valemi abil: kus ni = , nf= , ja lugeja iseloomustab tingimuslike keskmiste dispersiooni y, tingimusteta keskmisest y. On alati. Võrdsus = 0 vastab korreleerimata juhuslikele muutujatele; = 1 siis ja ainult siis, kui nende vahel on täpne funktsionaalne seos y ja x. Lineaarse seose korral y x-st kattub korrelatsioonisuhe korrelatsioonikordaja ruuduga. Väärtus - ? 2 kasutatakse regressiooni lineaarsusest kõrvalekaldumise indikaatorina. Korrelatsioonisuhe on korrelatsiooni mõõt y alates x mis tahes kujul, kuid ei saa anda aimu empiiriliste andmete erivormile lähendamise astmest. Et teada saada, kui täpselt konstrueeritud kõver empiirilisi andmeid peegeldab, võetakse kasutusele veel üks tunnus - determinismikordaja. Selle kirjeldamiseks võtke arvesse järgmisi koguseid. on ruutude kogusumma, kus on keskmine. Saame tõestada järgmist võrdsust Esimene liige on võrdne Sres = ja seda nimetatakse ruutude jääksummaks. See iseloomustab eksperimentaalsete kõrvalekaldeid teoreetilistest. Teine liige on võrdne Sreg = 2 ja seda nimetatakse ruutude regressioonisummaks ja see iseloomustab andmete levikut. On ilmne, et järgmine võrdsus S täis = S ost + S reg. Determinismi koefitsient määratakse järgmise valemiga: Mida väiksem on ruutude jääksumma võrreldes ruutude kogusummaga, seda suurem on determinismikordaja väärtus r2 , mis näitab, kui hästi seletab regressioonanalüüsi abil genereeritud võrrand muutujate vahelisi seoseid. Kui see on võrdne 1-ga, siis on mudeliga täielik korrelatsioon, s.t. tegelike ja hinnanguliste y väärtuste vahel pole vahet. Vastasel juhul, kui determinismikordaja on 0, ei suuda regressioonivõrrand y väärtusi ennustada Determinismikordaja ei ületa alati korrelatsioonikordajat. Juhul kui võrdsus r 2 = siis võime eeldada, et konstrueeritud empiiriline valem kajastab empiirilisi andmeid kõige täpsemalt. 2. Probleemi avaldus 1. Vähimruutude meetodit kasutades on tabelis määratud funktsioon ligikaudne a) esimese astme polünoom; b) teise astme polünoom; c) eksponentsiaalne sõltuvus. Iga sõltuvuse jaoks arvutage determinismi koefitsient. Arvutage korrelatsioonikordaja (ainult juhul a). Joonistage iga sõltuvuse jaoks trendijoon. Funktsiooni LINEST abil arvutage sõltuvuse arvkarakteristikud. Võrrelge oma arvutusi funktsiooni LINEST abil saadud tulemustega. Tehke järeldus, milline saadud valemitest vastab funktsioonile kõige paremini. Kirjutage programm ühes programmeerimiskeeles ja võrrelge arvutustulemusi ülaltoodud tulemustega. 3. Algandmed Funktsioon on toodud joonisel 1. 4. Lähenduste arvutamine tabelis Excel Arvutuste tegemiseks on soovitatav kasutada Microsoft Exceli tabelit. Ja korraldage andmed, nagu on näidatud joonisel 2. Selleks sisestame: · lahtritesse A6:A30 sisestame väärtused xi . · lahtritesse B6:B30 sisestame ui väärtused . · lahtrisse C6 sisestage valem =A6^ 2. · see valem kopeeritakse lahtritesse C7:C30. · Lahtrisse D6 sisestage valem =A6*B6. · see valem kopeeritakse lahtritesse D7:D30. · lahtrisse F6 sisestage valem =A6^4. · see valem kopeeritakse lahtritesse F7:F30. · lahtrisse G6 sisestame valemi =A6^2*B6. · see valem kopeeritakse lahtritesse G7:G30. · lahtrisse H6 sisestage valem =LN(B6). · see valem kopeeritakse lahtritesse H7:H30. · lahtrisse I6 sisestage valem =A6*LN(B6). · see valem kopeeritakse lahtritesse I7:I30. Teeme automaatse summeerimise abil järgmised sammud · lahtrisse A33 sisestage valem = SUM (A6: A30). · lahtrisse B33 sisestage valem = SUM (B6: B30). · lahtrisse C33 sisestage valem = SUM (C6: C30). · lahtrisse D33 sisestage valem = SUM (D6: D30). · lahtrisse E33 sisestage valem =SUM (E6:E30). · lahtrisse F33 sisestage valem = SUM (F6: F30). · lahtrisse G33 sisestage valem = SUM (G6: G30). · lahtrisse H33 sisestage valem = SUM (H6: H30). · lahtrisse I33 sisestage valem = SUM (I6: I30). Lähendame funktsiooni y=f(x) lineaarfunktsioon y=a1 + a2x. Koefitsientide määramiseks a 1ja a 2kasutame süsteemi (4). Kasutades tabeli 2 summasid, mis asuvad lahtrites A33, B33, C33 ja D33, kirjutame süsteemi (4) kui mille lahendamisel saame a 1= -24,7164 ja a2 = 11,63183 Seega on lineaarsel lähendusel vorm y = -24,7164 + 11,63183x (12) Süsteem (11) lahendati Microsoft Exceli abil. Tulemused on toodud joonisel 3: Tabeli lahtrid A38:B39 sisaldavad valemit (=NBR (A35:B36)). Rakud E38:E39 sisaldavad valemit (=MULTI(A38:B39, C35:C36)). Järgmisena lähendame funktsiooni y=f(x) ruutfunktsioon y=a1 + a2 x + a3 x2. Koefitsientide määramiseks a 1, a 2ja a 3kasutame süsteemi (5). Kasutades tabeli 2 kogusummasid, mis asuvad lahtrites A33, B33, C33, D33, E33, F33 ja G33, kirjutame süsteemi (5) järgmiselt: Mille lahendamisel saame a 1= 1,580946, a 2= -0,60819 ja a3 = 0,954171 (14) Seega on ruutlähendusel järgmine vorm: y \u003d 1,580946 -0,60819x + 0,954171 x2 Süsteem (13) lahendati Microsoft Exceli abil. Tulemused on toodud joonisel 4. Tabeli lahtrid A46:C48 sisaldavad valemit (=NBR (A41:C43)). Lahtrid F46:F48 sisaldavad valemit (=MULTI(A41:C43, D46:D48)). Nüüd lähendame funktsiooni y=f(x) eksponentsiaalfunktsioon y=a1 ea2x. Koefitsientide määramiseks a1 Ja a2 võta väärtuste logaritm yija kasutades tabeli 2 summasid, mis asuvad lahtrites A26, C26, H26 ja I26, saame süsteemi: kus с = ln(a1 ). Lahendussüsteemi (10) leiame c =0,506435, a2 = 0.409819. Pärast potentseerimist saame a1 = 1,659365. Seega on eksponentsiaalsel lähendusel vorm y = 1,659365*e0,4098194x Süsteem (15) lahendati Microsoft Exceli abil. Tulemused on näidatud joonisel 5. Tabeli lahtrid A55:B56 sisaldavad valemit (=NBR (A51:B52)). Lahtrid E54:E56 sisaldavad valemit (=MULTIPLE(A51:B52, C51:C52)). Lahter E56 sisaldab valemit =EXP(E54). Arvutage x ja y aritmeetiline keskmine, kasutades valemeid: Arvutustulemused x ja yMicrosoft Exceli tööriistad on näidatud joonisel 6. Lahter B58 sisaldab valemit =A33/25. Lahter B59 sisaldab valemit =B33/25. tabel 2 Selgitame, kuidas joonisel 7 kujutatud tabel koostatakse. Lahtrid A6:A33 ja B6:B33 on juba täidetud (vt joonis 2). · lahtrisse J6 sisestage valem =(A6-$B$58)*(B6-$B$59). · see valem kopeeritakse lahtritesse J7:J30. · lahtrisse K6 sisestage valem =(A6-$B$58)^ 2. · see valem kopeeritakse lahtritesse K7:K30. · lahtrisse L6 sisestage valem =(B1-$B$59)^2. · see valem kopeeritakse lahtritesse L7:L30. · lahtrisse M6 sisestage valem =($E$38+$E$39*A6-B6)^2. · see valem kopeeritakse lahtritesse M7:M30. · lahtrisse N6 sisestage valem =($F$46 +$F$47*A6 +$F$48*A6 L6-B6)^2. · see valem kopeeritakse lahtritesse N7:N30. · lahtrisse O6 sisestage valem =($E$56*EXP ($E$55*A6) - B6)^2. · see valem kopeeritakse lahtritesse O7:O30. Teeme automaatse summeerimise abil järgmised sammud. · lahtrisse J33 sisestage valem =CYMM (J6:J30). · lahtrisse K33 sisestage valem = SUM (K6: K30). · lahtrisse L33 sisestage valem =CYMM (L6:L30). · lahtrisse M33 sisestage valem = SUM (M6: M30). · lahtrisse N33 sisestage valem = SUM (N6: N30). · lahtrisse O33 sisestage valem = SUM (06:030). Nüüd arvutame valemi (8) abil korrelatsioonikordaja (ainult lineaarse lähenduse korral) ja determinismikordaja valemi (10) abil. Arvutuste tulemused Microsoft Exceli abil on näidatud joonisel 7. Tabelis 8 sisaldab lahter B61 valemit =J33/(K33*L33^(1/2). Lahter B62 sisaldab valemit =1 - M33/L33. Lahter B63 sisaldab valemit =1 - N33/L33. Lahter B64 sisaldab valem =1 - O33/L33. Arvutustulemuste analüüs näitab, et ruutlähendus kirjeldab kõige paremini katseandmeid. 4.1 Graafiku tegemine Excelis Valime lahtrid A1:A25, peale seda pöördume diagrammiviisardi poole. Valime hajusdiagrammi. Pärast diagrammi koostamist paremklõpsake diagrammi real ja valige trendijoone lisamine (vastavalt lineaarne, eksponentsiaalne, teise astme võimsus ja polünoom). Lineaarne lähendusgraafik Ruutarvulise lähendamise graafik Eksponentsiaalne sobiv joonis. 5. Funktsiooni lähendamine MathCADi abil Andmete lähendamine, võttes arvesse nende statistilisi parameetreid, viitab regressiooniprobleemidele. Tavaliselt tekivad need katseandmete töötlemisel, mis on saadud protsesside või füüsikaliste nähtuste mõõtmisel, mis on olemuselt statistilised (näiteks radiomeetria ja tuumageofüüsika mõõtmised) või kõrge interferentsi (müra) tasemega. Regressioonanalüüsi ülesanne on valida matemaatilised valemid, mis kirjeldavad kõige paremini katseandmeid. .1 Lineaarne regressioon Lineaarne regressioon Mathcad süsteemis teostatakse argumendi vektoritel Xja lugemised Y funktsioonid: pealtkuulamine (x, y)- arvutab parameetri aga1 , regressioonijoone vertikaalne nihe (vt joonis). kalle (x, y)- arvutab parameetri a2 , regressioonisirge kalle (vt joonist) y(x) = a1+a2*x Funktsioon õige(y, y(x))arvutab Pearsoni korrelatsioonikordaja.Mida lähemal ta on 1, seda täpsemalt vastavad töödeldavad andmed lineaarsele seosele (vt joonis). .2 Polünoomi regressioon Ühemõõtmelist polünoomi regressiooni polünoomi suvalise astmega n ja suvaliste valimikoordinaatidega Mathcadis teostavad funktsioonid: regress(x, y, n)- arvutab vektori S,mis sisaldab koefitsiente aipolünoom n aste; Koefitsiendi väärtused aisaab vektorist eraldada Sfunktsiooni alammaatriks (S, 3, pikkus(S) - 1, 0, 0). Saadud koefitsientide väärtusi kasutatakse regressioonivõrrandis y(x) = a1+a2*x+a3*x2 (vaata pilti.) .3 Mittelineaarne regressioon Lihtsate tüüpiliste lähendusvalemite jaoks on ette nähtud hulk mittelineaarseid regressioonifunktsioone, milles funktsiooni parameetrid valib programm Mathcad. Nende hulgas on funktsioon expfit(x, y, s),mis tagastab koefitsiente sisaldava vektori a1, a2Ja a3eksponentsiaalne funktsioon y(x) = a1 ^exp (a2x) + a3.V vektor Ssisestatakse koefitsientide algväärtused a1, a2Ja a3esimene lähendus. Järeldus Arvutustulemuste analüüs näitab, et lineaarne lähendus kirjeldab kõige paremini katseandmeid. Programmi MathCAD abil saadud tulemused vastavad täielikult Exceli abil saadud väärtustele. See näitab arvutuste õigsust. Bibliograafia
ÕpetamineVajad abi teema õppimisel?
Meie eksperdid nõustavad või pakuvad juhendamisteenust teile huvipakkuvatel teemadel. Eksperimentaalsete andmete lähendamine on meetod, mis põhineb katseliselt saadud andmete asendamisel analüütilise funktsiooniga, mis läbib või langeb sõlmpunktides kõige lähemalt algväärtustele (katse või katse käigus saadud andmed). Praegu on analüütilise funktsiooni määratlemiseks kaks võimalust: Konstrueerides n-kraadise interpolatsioonipolünoomi, mis läbib otse läbi kõigi punktide antud andmemassiivi. Sel juhul esitatakse lähendusfunktsioon järgmiselt: interpolatsioonipolünoom Lagrange'i kujul või interpolatsioonipolünom Newtoni kujul. Konstrueerides n-kraadise lähenduspolünoomi, mis läbib punktide lähedal antud andmemassiivist. Seega ühtlustab ligikaudne funktsioon kõik juhuslikud mürad (või vead), mis võivad katse ajal tekkida: katse ajal mõõdetud väärtused sõltuvad juhuslikest teguritest, mis kõikuvad vastavalt oma juhuslikele seaduspäradele (mõõtmis- või instrumendivead, ebatäpsus või katselised vead). vead). Sel juhul määratakse ligikaudne funktsioon vähimruutude meetodil. Vähima ruudu meetod(ingliskeelses kirjanduses Ordinary Least Squares, OLS) on matemaatiline meetod, mis põhineb ligikaudse funktsiooni määratlusel, mis on üles ehitatud antud katseandmete massiivi punktide lähimasse lähedusse. Alg- ja lähendusfunktsioonide F(x) lähedus määratakse numbrilise mõõduga, nimelt: katseandmete ruudus hälvete summa lähenduskõverast F(x) peaks olema väikseim. Vähimruutude meetodil koostatud sobituskõver Kasutatakse vähimruutude meetodit: Ülemääratud võrrandisüsteemide lahendamiseks, kui võrrandite arv ületab tundmatute arvu; Otsida lahendust tavaliste (mitte ülemääratletud) mittelineaarsete võrrandisüsteemide puhul; Punktväärtuste lähendamiseks mõne lähendusfunktsiooni abil. Vähimruutude meetodil lähendav funktsioon määratakse antud katseandmete massiivi arvutatud lähendusfunktsiooni hälbete miinimumsumma tingimusest. See vähimruutude meetodi kriteerium on kirjutatud järgmise avaldisena:
Arvutatud lähendusfunktsiooni väärtused sõlmpunktides, Määratud massiiv katseandmeid sõlmepunktides. Ruutkriteeriumil on mitmeid "häid" omadusi, nagu diferentseeritavus, mis pakub polünoomide lähendusfunktsioonidega aproksimeerimisprobleemile ainulaadse lahenduse. Sõltuvalt ülesande tingimustest on lähendusfunktsioon polünoom astmega m Lähendamisfunktsiooni aste ei sõltu sõlmpunktide arvust, vaid selle mõõde peab alati olema väiksem kui antud katseandmete massiivi dimensioon (punktide arv).
∙ Kui lähendava funktsiooni aste on m=1, siis lähendame tabelifunktsiooni sirgjoonega (lineaarne regressioon). ∙ Kui lähendusfunktsiooni aste on m=2, siis lähendame tabelifunktsiooni ruutparabooliga (ruutlikviatsioon). ∙ Kui lähendava funktsiooni aste on m=3, siis lähendame tabelifunktsiooni kuupparabooliga (kuupproksimatsioon). Üldjuhul, kui antud tabeliväärtuste jaoks on vaja konstrueerida ligikaudne polünoom kraadiga m, kirjutatakse kõigi sõlmpunktide hälvete minimaalse ruudusumma tingimus ümber järgmisel kujul:
Määratud tabeli väärtuste arv. Funktsiooni miinimumi olemasolu vajalik tingimus on selle osatuletise võrdsus nulliga tundmatute muutujate suhtes
Teisendame saadud lineaarset võrrandisüsteemi: avage sulud ja liigutage vabad liikmed avaldise paremale poole. Selle tulemusena kirjutatakse saadud lineaarsete algebraavaldiste süsteem järgmisel kujul:
Seda lineaarsete algebraavaldiste süsteemi saab maatriksi kujul ümber kirjutada:
Selle tulemusena saadi lineaarvõrrandi süsteem mõõtmetega m + 1, mis koosneb m + 1 tundmatust. Seda süsteemi saab lahendada mis tahes lineaarsete algebraliste võrrandite lahendamise meetodiga (näiteks Gaussi meetod). Lahenduse tulemusena leitakse aproksimeeriva funktsiooni tundmatud parameetrid, mis annavad minimaalse lähendusfunktsiooni ruutude hälbete summa algandmetest, s.o. parim võimalik ruutlähendus. Tuleb meeles pidada, et kui algandmete isegi üks väärtus muutub, muudavad kõik koefitsiendid oma väärtusi, kuna need on täielikult määratud algandmetega. Algandmete lähendamine lineaarse sõltuvuse järgi (lineaarne regressioon) Vaatleme näiteks ligikaudse funktsiooni määramise meetodit, mis on antud lineaarse seosena. Vähimruutude meetodi kohaselt kirjutatakse hälvete ruutude miinimumsumma tingimus järgmiselt: Tabeli sõlmpunktide koordinaadid; Lähendava funktsiooni tundmatud koefitsiendid, mis on määratud lineaarse seosena. Funktsiooni miinimumi olemasolu vajalik tingimus on selle osatuletise võrdsus nulliga tundmatute muutujate suhtes. Selle tulemusena saame järgmise võrrandisüsteemi:
Teisendame saadud lineaarse võrrandisüsteemi.
Lahendame saadud lineaarvõrrandisüsteemi. Lähendava funktsiooni koefitsiendid analüütilisel kujul määratakse järgmiselt (Crameri meetod):
Need koefitsiendid võimaldavad luua lineaarse lähendusfunktsiooni vastavalt kriteeriumile, mille eesmärk on minimeerida ligikaudse funktsiooni ruutude summa antud tabeliväärtustest (eksperimentaalsed andmed). Algoritm vähimruutude meetodi rakendamiseks 1. Algandmed: Arvestades eksperimentaalsete andmete massiivi mõõtmiste arvuga N On antud lähendava polünoomi aste (m). 2. Arvutusalgoritm: 2.1. Mõõtmetega võrrandisüsteemi koostamiseks määratakse koefitsiendid
Võrrandisüsteemi koefitsiendid (võrrandi vasak pool)
Lineaarvõrrandisüsteemi vabaliikmed (võrrandi parem pool)
2.2. Mõõtmega lineaarvõrrandisüsteemi moodustamine .
2.3. Lineaarvõrrandisüsteemi lahendamine astme m lähendava polünoomi tundmatute kordajate määramiseks. 2.4 Lähendava polünoomi algväärtustest kõigi sõlmepunktide ruudu hälvete summa määramine
Ruuthälvete summa leitud väärtus on minimaalne võimalik. Ühtlustamine muude funktsioonidega Tuleb märkida, et algandmete lähendamisel vastavalt vähimruutude meetodile kasutatakse mõnikord lähendava funktsioonina logaritmilist funktsiooni, eksponentsiaalfunktsiooni ja võimsusfunktsiooni. Logi ligikaudne Mõelge juhtumile, kui ligikaudne funktsioon on antud vormi logaritmilise funktsiooniga: | ||